Nejen pro maturanty…
Zápis k videím
Zopakujte si – převody jednotek, rychlost
- převody jednotek – sbírka úloh
- převody jednotek – videa youtube: začátek playlistu (označení FS-1.0)
- rychlost – sbírka úloh
- pracovní list – ke grafům s(t) doplňte graf v(t) či naopak.
- Tento Powerpointový soubor (pro učitele) ukazuje některé typické grafy polohy x(t), které můžete využít při výuce kinematiky – rychlost, zrychlení, atp.
Zrychlení
Dráha rovnoměrně zrychleného pohybu
quizizz: dráha jako obsah pod křivkou
Volný pád a vrh svislý
Vrh vodorovný
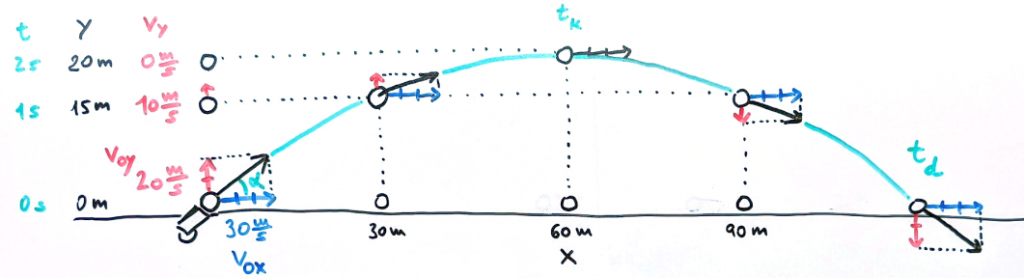
Vrh šikmý
Shrnutí a vztahy
- Rychlost a zrychlení: přímočarý pohyb: $v = \Delta s/\Delta t$, $a = \Delta v/\Delta t$.
- Rychlost rovnoměrně zrychleného pohybu: $v = v_0 + at$, kde $v_0$ je počáteční rychlost, $a$ je konstantní zrychlení a $t$ je čas.
- Dráha rovnoměrně zrychleného pohybu: $s = s_0 + v_0t + \frac{1}{2}at^2$, kde $s_0$ je počáteční dráha, $v_0$ je počáteční rychlost, $t$ je čas a $a$ je konstantní zrychlení. Platí i pro zpomalený pohyb, kdy je $a$ záporné. Speciální případ je zrychlování z nulové rychlosti, nebo zpomalování do nulové rychlosti, kdy se vztah pro dráhu redukuje na $s = \frac{1}{2}at^2$.
- Pro výpočet dráhy při rovnoměrně zrychleném pohybu je také vždy možné užit vztah $s = v_p t$, kde $v_p$ je průměrná rychlost při pohybu. Často nám toto uvažování usnadní práci.
- Nemá smysl zde uvádět vztahy pro vrhy, jako vztah pro dopadovou rychlost, výšku výstupu, dobu letu, délku hodu atp. Má smysl si umět tyto vztahy vždy odvodit!
Návrhy na experimenty
- Měření výšky pomocí míčku. Dejte míček do výše své hlavy a stopněte, jak dlouho trvá, než dopadne. Na základě toho spočítejte svou výšku? Jak přesné toto měření je? Jakým způsobem je potřeba čas měřit, aby byl co nejpřesnější?
- Měření reakční doby pravítkem. Jeden člověk vezme na vrchním konci pravítko (případně svinovací metr) do svislé polohy. Druhý člověk dá prsty těsně k pravítku na rysce cca 30 cm. První člověk v nestřežený okamžik pravítko upustí a druhý člověk se ho snaží okamžitě chytit. Na základě toho, o kolik se pravítko propadlo, určete reakční čas člověka, který pravítko chytal.
- Je čůrek parabola? V láhvi udělejte v její dolní polovině díru, napusťte do ní vodu a dejte na vyvýšené místo. Nechte vodu odtékat do nějaké nádoby. Vyfoťte proud vody. Ve vhodném softwaru odečtěte souřadnice bodů čůrku vody. V tabulkovém editoru či v nějaké internetové kalkulačce se pokuste zjistit, zda má čůrek vody tvar paraboly.
- Vzdálenost dostřiku. V láhvi udělejte v její dolní polovině díru, napusťte do ní vodu a dejte na vyvýšené místo. Nechte odtékat do umyvadla či do nějaké nádoby. Měřte závislost vzdálenosti dostřiku na výšce hladiny nad dírou a vyneste do grafu. Ověřte také, zda vzdálenost dostřiku odpovídá výpočtu pro vodorovný vrh. Lze předpokládát, že voda z otvoru vystřikuje rychlostí $v = \sqrt{2gh}$, kde $h$ je výška hladiny nad otvorem, tedy rychlost vystřikování je stejná, jako je dopadová rychlost volného pádu z výšky $h$.