$\newcommand{\tdot}{\!\cdot\!}
\newcommand{\jv}{\,\mathrm{m \tdot s^{-1}}}
\newcommand{\jp}{\,\mathrm{kg \tdot m \tdot s^{-1}}}
\newcommand{\kmh}{\,\mathrm{km \tdot h^{-1}}}
\newcommand{\ja}{\,\mathrm{m \tdot s^{-2}}}
\newcommand{\jN}{\,\mathrm{N}}
\newcommand{\jkg}{\,\mathrm{kg}}
\newcommand{\js}{\,\mathrm{s}}
\newcommand{\jm}{\,\mathrm{m}}
\newcommand{\–}{\mathbin{-}}$
Veličiny a jednotky
Při přívalovém dešti v italském městě Tutti Mangiano spadlo 50 litrů srážek na metr čtverečný. Vyjádřete úhrn srážce jako výšku sloupce v mm.
Jedná se o to, že na ploše S = 1 m2 bude ležet kvádr vody o celkovém objemu V = 50 litrů. Nás zajímá výška h tohoto kvádru. Tu lze vyjádřit jako h = V/S = 50 litrů / 1 m2, což lze zapsat jako h = 50 dm3/m2.
Jednotky musíme dát do souladu: h = 50 dm3/m2 = 50 dm3 / 100 dm2 = 0,5 dm.
Výška kvádru je 0,5 dm = 50 mm, což odpovídá výšce vodního sloupce. Vidíme tedy, že údaj v litrech na m2 a údaj v milimetrech srážek mají stejnou číselnou hodnotu.
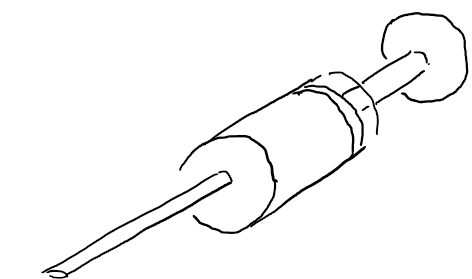
Zdravotní sestra Cassandra zachraňuje životy. Má roztok atropinu v koncentraci 0,5 g/litr a injekční stříkačku o průměru 12 mm. O jakou vzdálenost musí stlačit píst stříkačky, aby pacientovi vpravila 2 mg atropinu? Zvládnete život zachránit i vy, nebo pacienta zabijete v důsledku neznalosti převodů jednotek?
Převedeme koncentraci na mg/ml:
$0,5 \, \text{g/litr} = 500 \, \text{mg/litr} = 0,5 \, \text{mg/ml}$
To znamená, že v každém mililitru roztoku je $0,5 \, \text{mg}$ atropinu.
Aby sestra vpravila $2 \, \text{mg}$ atropinu, musíme proto použít 4 ml roztoku, což je 4 cm3 roztoku.
Průměr stříkačky je 12 mm a poloměr 6 mm, čili 0,6 cm.
$V = S \cdot h = \pi r^2 \cdot h$, kde $h$ je délka (vzdálenost), o kterou je potřeba stlačit píst.
Plocha průřezu je tedy 1,13 cm2.
Ze vztahu pro objem vyjádříme $h = V/S = 4\,\text{cm}^3 / 1,13\,\text{cm}^2 = 3,54 cm$.
Všimněme si, že nebylo potřeba počítat v základních jednotkách – bylo pohodlné vše vyjadřovat v cm.
Cassandra musí píst stlačit o 3,54 cm, neboli 35,4 mm.
Na pneumatice je uvedeno “inflate to 50 psi”. PSI znamená “pounds per square inch”. Vyjádřete v jednotkách běžného metrického systému, tedy jako kg/m2. Jakou veličinu vlastně tato jednotka určuje?
Nejprve převedeme $50 \, \text{psi}$ do jednotek $ \text{kg/m}^2 $.
1 pound (libra) je přibližně $0,4536 \, \text{kg}$ a 1 inch (palec) je $0,0254 \, \text{m}$.
Plocha jednoho čtverečního palce je tedy:
$1 \, \text{inch}^2 = (0,0254 \, \text{m})^2 = 6,4516 \times 10^{-4} \, \text{m}^2$
Nyní převedeme $50 \, \text{psi}$:
$50 \, \text{psi} = \frac{50 \, \text{pounds}}{1 \, \text{inch}^2}$
Dosadíme za pounds a inch:
$50 \, \text{psi} = \frac{50 \times 0,4536 \, \text{kg}}{6,4516 \times 10^{-4} \, \text{m}^2}$
Vypočítáme hodnotu:
$50 \, \text{psi} = \frac{22,68 \, \text{kg}}{6,4516 \times 10^{-4} \, \text{m}^2} \approx 35 150 \, \text{kg/m}^2$
Tlak $50 \, \text{psi}$ je tedy přibližně $35 150 \, \text{kg/m}^2$.
Jednotka PSI určuje tlak, ale ve skutečnosti to není v pravém smyslu jednotka tlaku. Abychom mohli hodnotu převést na Pascaly, je ještě nutné výsledek přeenásobit gravitačním zrychlením g, abychom z hmotnosti na plochu dostali tíhovou sílu na plochu. Pak nám vyjde, že odpovídající tlak je asi 350 kPa, tedy asi 3,5 atm.
Ponorka vyjela v čase 8:41:37 a do cíle dorazila v 11:14:26. Vyjádřete dobu jízdy v hodinách jako desetinné číslo.
Od startu do 9:00:00 zbývá 23 sekund a 18 minut. Poté jsou dvě celé hodiny do 11:00:00. a zbývá 14 minut a 26 sekund. Celkem tedy 2h 32 min 49 s. Počet hodin je to
$2 + 32/60 + 49/3600 = 2,547\,\text{h}$.

a) Odvoďte převodní vztah mezi jednotkami hustoty kg/m3 a g/cm3, tedy 1 g/cm3 = …
b) Odvoďte převodní vztah mezi km/h a m/s, tedy 1 m/s = …
a) 1 m je 100-krát větší než 1 cm, tedy 1 m3 bude 1003x = 106x větší než 1 cm3. Milionkrát větší objem bude mít milionkrát větší hmotnost, tedy milion gramů, což je 1000 kg.
Proto 1 g/cm3 = 1000 kg/m3.
b) Pokud urazím za 1 sekundu jeden metr, tak za hodinu, což je 3600 s, urazím úměrně delší vzdálenost, tedy 3600 m = 3,6 km. Proto
1 m/s = 3,6 km/h.
Vžijte se do světa, kde základní jednotkou času je den a základní jednotkou vzdálenosti je astronomická jednotka (AU), čili vzdálenost Země-Slunce (asi $150\times10^6\,\text{km}$). Jakou hodnotu pak bude mít rychlost světla?
$1\,\text{AU} = 1,5 \times 10^{11}\,\text{m}$, 1 den = 86400 s, rychlost světla je $c \approx 3 \times 10^8\,\text{m/s}$.
Potom
$c = 3 \times 10^8\,\text{m/s} = \frac{3 \times 10^8 : 1,5 \times 10^{11}\cdot\text{AU}}{1:86400\cdot\text{den}} = 2\times10^{-3}\cdot 86400 \,\text{AU/den} = 172,8 \,\text{AU/den}$.
Mějme dvě síly, tedy dva vektory, o velikosti 2 N a 1 N, které působí na ořech. Mohou působit různými směry.
a) Jaká je max. a min. velikost jejich výslednice?
b) Jakou velikost má výslednice, působí-li na sebe kolmo?
c) Jaká musí být úhlová odchylka směru sil, pokud má výslednice stejnou velikost jako větší síla, tedy 2 N?
a) Maximálně 3 N, minimálně 1 N.
b) Při kolmém působení $F = \sqrt{2^2 + 1^2} = \sqrt{5}\,\text{N} = 2,24\,\text{N}$.
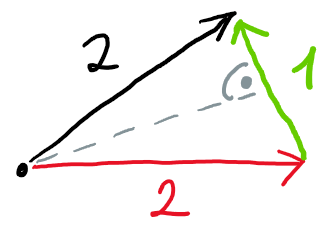
c) Zřejmě odchylka sil musí být větší než 90°, tedy síly musí svírat tupý úhel. Můžeme si ale všimnout, že síly F1, F2 a jejich výslednice vlastně tvoří rovnoramenný trojúhelník, protože výslednice a síla F1 mají stejnou velikost. Máme tedy rovnoramenný trojúhelník o délkách stran 2; 2; 1. Tento trojúhelník můžeme rozdělit na dva pravoúhlé trojúhelníky, jehož přepona má délku 2 a kratší odvěsna délku 1/2. Pro hledaný úhel pak platí $\alpha = 180° – \cos(0,5/2) = 104,48°$.
Úlohu můžeme samozřejmě řešit i přímo na základě cosinové věty: $c^2 = a^2 + b^2 – 2ab\cos\gamma$. Přenecháváme čtenáři.
Rychlost
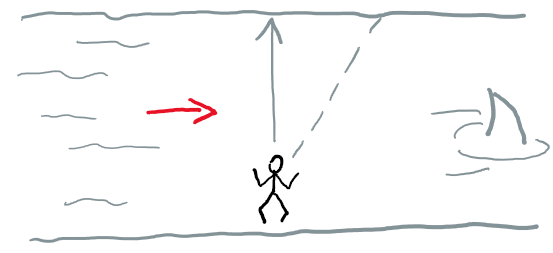
Tereza plave přes Labe, protože spadl most. Proud má rychlost 2 km/h a v klidné vodě Terka plave rychlostí 4 km/h. Labe je široké 60 m.
a) Pokud se Terka bude snažit dostat na druhý břeh co nejdříve, jak dlouho ji to bude trvat? Jaká bude její rychlost vůči zemi?
b) Pokud Terka bude plavat tak, aby se její tělo neustále pohybovalo kolmo k břehu, jak dlouho ji to bude trvat? Pod jakým úhlem musí mít natočené tělo, aby se pohybovala pořád kolmo k břehu?
a) Nejrychleji se na druhý břeh dostane, když bude plavat kolmo k proudu (tedy vzhledem k břehu se bude pohybovat šikmo, částečně směrem po proudu, protože proud ji unáší. Její rychlost kolmo k proudu je $v_k = 4\,\text{km/h}$ a to je také rychlost, jakou se bude zvětšovat její kolmá vzdálenost od břehu. Labe tedy překoná v čase $t = s/v_k = \text{60 / (4:3,6)= 54 s}$.
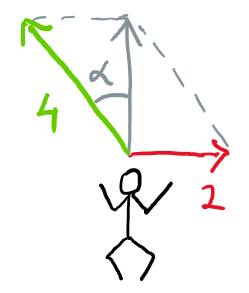
b) Terka se musí natočit trochu proti proudu tak, aby složka její vlastní rychlosti proti proudu byla 2 km/h, tedy stejná jako je rychlost proudu. Pro úhel natočení od směru kolmého na břeh tedy musí platit $\sin\alpha = 2/4$, tedy $\alpha = \sin^{-1}(1/2) = 30°$. Složka její rychlosti kolmo k břehu bude $v_k = \cos30°\cdot 4\,\text{km/h}$ a doba potřebná k přeplavání bude $t = s/v_k$. Dosazením dostaneme 62 sekund.
Můžeme si také všimnout, že rychlost vzdalování od břehu je $v = \sqrt{v^2_1 – v^2_2}$, kde $v_1$ a $v_2$ jsou rychlost Terky a rychlost proudu.
Anakin každé ráno leze na Milešovku, aby se podíval zblízka na oblaka. Cestou nahoru jde rychlostí 3 km/h, nahoře se hned otočí a cestou dolů běží rychlostí 6 km/h. Jaká je jeho průměrná rychlost na celé trase?
Nesmíme se nechat zmást a tipnout, že průměrná rychlost je 4,5 km/h – tak to není. Průměrná rychlost je rovna “celková dráha” / “celkový čas”. Délku jednosměrné cesty na Milešovku si můžeme zvolit libovolnou, výsledek bude na této volbě nezávislý. Volme třeba 1 km. Potom $v_p = 2 / (1/3 + 1/6) = 2 / (0,5) = 4\,\text{km/h}$. Můžeme si všimnout, že výsledek je harmonickým průměrem zadaných rychlostí.
Loď Helmut pluje po řece z Prasákova do Sviňákova po proudu a cesta trvá 40 minut. Zpět pluje proti proudu a cesta trvá 70 minut. Jak dlouho by lodi trvalo ujet stejnou vzdálenost, kdyby plula po klidné hladině?
Rychlost lodi proti proudu označme $v_1$. Rychlost na klidné vodě pak bude $v_1 + v_p$, rychlost po proudu $v_1 + 2v_p$. Poměr $(v_1+2v_p)/v_1 = 7/4$. Tedy $v_p/v_1 = 0,375$. Odtud plyne, že $(v_1+v_p)/v_1 = 1,375$. Cesta na klidné vodě tak bude trvat $1,375\times$ kratší dobu, než proti proudu, tedy hledaný čas je t = 70 min / 1,375 = 51 minut.
Upozorněme, že výsledek je harmonický průměr čísel 40 a 70.
Alík vyjíždí z Prahy do Brna rychlostí 130 km/h, zatímco Baryk vyjíždí z Brna rychlostí 100 km/h. Vzdálenost Praha Brno budiž 200 km.
a) Za jak dlouho se setkají, pokud vyrazí současně?
b) Na kolikátem kilometru se potkají, pokud Alík vyjede o půl hodiny později?
a) Dráha $s = v_A t + v_B t$, čili $t = s/(v_A + v_B)$ = 200 km / (230 km/h) = 0,87 h, čili něco přes 52 minut.
b) Berme to tak, že Baryk jede o půl hodiny déle, tedy platí $s = v_A t + v_B (t + 0,5)$, čili
$t = (s – 0,5\cdot v_B) / (v_A + v_B)$ = 0,65 h.
To je doba jízdy Alíka, za kterou urazí vzdálenost 84,8 km. Samozřejmě vidíme, že po půlhodině jízdy Baryka se jejich vzdálenost zmenšila na 150 km a tím úlohu převedeme na předchozí případ, kdy vyraží současně.

Rumcajs vyběhl ze zámku a běží rychlostí 5 m/s. Za 10 minut po něm vyběhl Cipísek, který má mladé hnáty a běží rychlostí 8 m/s. Jak daleko od zámku Rumcajse dohoní? Řešte početně i graficky!
Rumcajs má náskok 10 minut=600 s a za tuto dobu uběhne 3000 m. Vzájemná rychlost Cipíska a Rumcajse je 8-5 = 3 m/s. Touto rychlostí bude Cipísek ukrajovat Rumcajsův náskok a bude mu to trvat zřejmě 1000 s, čili 16 minut a 40 sekund. Cipísek běží od zámku po dobu 1000 s rychlostí 8 m/s a tedy Cipísek Rumcajse dohoní 8000 m od zámku, čili 8 km.
Arnold nejprve půl hodiny běží rychlostí 10 km/h, poté dvě hodiny plave rychlostí 3 km/h, následně půl hodiny obědvá ve školní jídelně a nakonec dvacet minut jede na kole rychlostí 24 km/h. Nakreslete graf závislosti v(t) a s(t).
Přenecháváme laskavému čtenáři.
Zrychlení
Formule F1 zrychlí z 0 na 100 km/h zhruba za 2,5 sekundy. Jaké je její průměrné zrychlení? Pozor na jednotky.
Nejprve převedeme rychlost z km/h na m/s:
$v = 100 \, \text{km/h} = 100 : 3,6 \, \text{m/s} = 27,78 \, \text{m/s}$.
Formule se rozjíždí z klidu a její změna rychlosti je tedy právě $\Delta v = 27,78\,\text{m/s}$.
Průměrné zrychlení $a$ je dáno vztahem:
$a = \frac{\Delta v}{\Delta t} = \frac{27,78 \, \text{m/s}}{2,5 \, \text{s}} = 11,11 \, \text{m/s}^2$
Průměrné zrychlení je tedy přibližně $11,11 \, \text{m/s}^2$.
Všimněme si, že to je více než gravitační zrychlení. Pokud bychom s běžným autem chtěli tolik zrychlit, zahrabaly by kola. K takovémuto zrychlení jsou potřeba speciální pneumatiky, snížené těžiště, zvýšený přítlak atp.
Auto jedoucí rychlostí 50 km/h prudce brzdí se zrychlením – 4 m/s2. Za jak dlouho zpomalí na 20 km/h?
Změna rychlosti je o $\Delta v = 30\,\text{km/h} = 8,33\,\text{m/s}$.
Rychlost se každou sekundu změní o $a = 4\,\mathrm{m/s^2}$.
Proces změny rychlosti tedy bude trvat
$t = \frac{\Delta v}{a} = \frac{8,33}{4} = 2,08 \, \text{s}$
Auto zpomalí na $20 \, \text{km/h}$ za přibližně $2,08 \, \text{s}$.
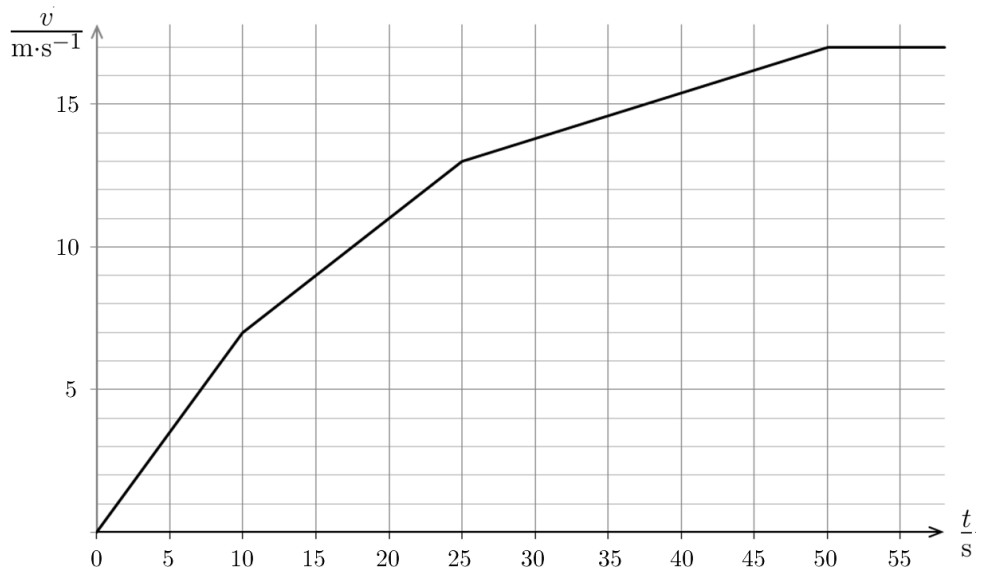
Určete zrychlení vlaku v jednotlivých úsecích na základě grafu v(t). [kredit: Fyzikální olympiáda]
Na každém úseku odečteme změnu rychlosti a změnu času, pak $a = \Delta v / \Delta t$. Zrychlení jsou postupně 7/10, 6/15, 4/25 a 0 m/s2.
Počítejte následující úlohy (bez kalkulačky):
a) Tadej Pogačar během pěti sekund zrychlil z 6 m/s na 14 m/s. Jaké je jeho zrychlení?
b) Tramvaj jela počáteční rychlostí 4 m/s a po dobu půl minuty zrychlovala se zrychlením 0,5 m/s2. Jaká byla její výsledná rychlost?
c) Ze smrku spadla šiška na zem. Pád trval 1,4 sekundy. Jakou rychlostí šiška dopadla?
d) Vlak po dobu jedné minuty zrychloval se zrychlením 0,3 m/s2, až dosáhl rychlosti 30 m/s. Jaká byla jeho počáteční rychlost?
e) Auto při najíždění na dálnici zrychlilo ze 72 km/h na 126 km/h, přičemž jeho zrychlení bylo 2,5 m/s2. Určete, za jak dlouho auto výsledné rychlosti dosáhlo. Nezapomeňte na převod jednotek!
f) Auto jedoucí rychlostí 54 km/h prudce brzdí se zrychlením – 4 m/s2. Za jak dlouho zastaví?
a) Použijeme rovnici pro zrychlení:
$a = \frac{\Delta v}{\Delta t} = \frac{v – v_0}{t}$
Dosadíme hodnoty:
$a = \frac{14 \, \text{m/s} – 6 \, \text{m/s}}{5 \, \text{s}} = \frac{8 \, \text{m/s}}{5 \, \text{s}} = 1,6 \, \text{m/s}^2$
Tadejovo zrychlení je tedy $1,6 \, \text{m/s}^2$.
b) Použijeme rovnici:
$v = v_0 + a t$
Dosadíme hodnoty:
$v = 4 \, \text{m/s} + 0,5 \, \text{m/s}^2 \times 30 \, \text{s} = 4 \, \text{m/s} + 15 \, \text{m/s} = 19 \, \text{m/s}$
Výsledná rychlost tramvaje byla $19 \, \text{m/s}$.
c) $v = gt$, tedy výsledná rychlost 14 m/s.
d) $v = v_0 + at$, tedy $v_0 = v – at = 30 – 0,3 \cdot 60 = 12\,\text{m/s}$.
e) Nejprve převedeme rychlosti z km/h na m/s:
$v_0 = 72 \, \text{km/h} = 20 \, \text{m/s}$
$v = 126 \, \text{km/h} = 35 \, \text{m/s}$
Celková změna rychlosti byla 15 m/s. Každou jednu sekundu se rychlost změní o 2,5 m/s. Změna rychlosti tak bude celkem trvat
$t = \frac{\Delta v}{a} = \frac{35 \, \text{m/s} – 20 \, \text{m/s}}{2,5 \, \text{m/s}^2} = \frac{15 \, \text{m/s}}{2,5 \, \text{m/s}^2} = 6 \, \text{s}$
Auto dosáhne výsledné rychlosti za 6 sekund.
f) Nejprve převedeme rychlost z km/h na m/s:
$v_0 = 54 \, \text{km/h} = 15 \, \text{m/s}$
Použijeme rovnici pro zrychlení:
$t = \frac{\Delta v}{a} = \frac{15 \, \text{m/s}}{4 \, \text{m/s}^2} = 3,75 \, \text{s}$
Auto zastaví za 3,75 sekundy.
Dráha zrychleného pohybu
Karolína stojí nad propastí a upustí do ní kámen. Kámen dopadl na dno po čtyřech sekundách letu. a) Jak hluboká je propast? Mohla by to být Macocha? Diskutujte.
b) Jakou rychlostí kámen dopadl na zem?
c) Nakreslete graf uražené dráhy v závislosti na čase, tedy určete celkovou uraženou dráhu po uplynutí 1 s, 2 s, 3 s a 4 s.
a) Jak hluboká je propast?
Pro výpočet hloubky propasti použijeme rovnici pro volný pád:
$h = \frac{1}{2} g t^2$
kde:
$h$ = hloubka propasti,
$g$ = gravitační zrychlení $(9,81 \, \text{m/s}^2)$,
$t$ = čas pádu $(4 \, \text{s})$.
Dosadíme hodnoty:
$h = \frac{1}{2} \times 9,81 \, \text{m/s}^2 \times (4 \, \text{s})^2 = 0,5 \times 9,81 \, \text{m/s}^2 \times 16 \, \text{s}^2 = 78,48 \, \text{m}$
Hloubka propasti je tedy přibližně $78,5 \, \text{m}$.
Macocha je hluboká asi $138 \, \text{m}$, takže propast nemůže být Macocha.
b) Jakou rychlostí kámen dopadl na zem?
Použijeme rovnici pro rychlost při volném pádu:
$v = g t$
Dosadíme hodnoty:
$v = 9,81 \, \text{m/s}^2 \times 4 \, \text{s} = 39,24 \, \text{m/s}$
Rychlost, kterou kámen dopadl na zem, je přibližně $39,2 \, \text{m/s}$.

Ondra pouští klíče Martinovi ze čtvrtého patra (11 metrů nad Martinovou hlavou). Za jak dlouho po upuštění klíče Martinovi rozrazí hlavu? Bude mít čas odříkat si otčenáš?
Pro výpočet času pádu použijeme rovnici pro volný pád:
$h = \frac{1}{2} g t^2$
kde:
$h = 11 \, \text{m}$ je výška, ze které jsou klíče puštěny,
$g = 9,81 \, \text{m/s}^2$ je gravitační zrychlení,
$t$ je čas pádu, který hledáme.
Vyjádříme čas $t$:
$t = \sqrt{\frac{2h}{g}}$
Dosadíme hodnoty:
$t = \sqrt{\frac{2 \times 11 \, \text{m}}{9,81 \, \text{m/s}^2}} = \sqrt{\frac{22}{9,81}} = \sqrt{2,24} \approx 1,5 \, \text{s}$
Klíče dopadnou za přibližně $1,5 \, \text{s}$.
Pokud by Martin chtěl za tu dobu odříkat Otčenáš, zřejmě to nestihne, protože modlitba trvá okolo 15–20 sekund.
Štepán si přál k Vánocům, aby byl 100x větší. Přání se mu splnilo a nyní měří na výšku 170 metrů. Na oslavu této velké události hned z výšky svého majestátu, tedy z výšky 170 m, upustil kámen. Neuvažujte odpor vzduchu, berte g=10 m/s2 a odpovězte na otázky:
a) V jaké výšce nad zemí se kámen nachází 2,5 sekundy po vypuštění?
b) Za jak dlouho bude kámen ve výšce 100 m?
c) Jakou rychlostí kámen poletí ve výšce 100 m?
d) Jakou dráhu urazí kámen během čtvrté sekundy letu?
e) Jakou rychlostí kámen dopadne na zem?
f) V jaké výšce bude kámen ve chvíli, kdy letí rychlostí 50 m/s?
a) $s=\frac{1}{2}gt^2 = \frac{1}{2} \cdot 10 \cdot 2,5^2 = 31,25\jm$. V tu chvíli bude ve výšce h = 170 m – 31,25 m = 138,75 m.
b) Uražená dráha je 70 m. Platí $s=\frac{1}{2}gt^2$. Vyjádříme čas: $t = \sqrt{\frac{2s}{g}} = \sqrt{\frac{2\cdot70}{10}} = \sqrt{\frac{2\cdot70}{10}} = \sqrt{14} = 3,74\js$.
c) Letí po dobu 3,74 s, $v = gt = 37,4\jv$.
d) Čtvrtá sekunda začíná časem t1 = 3 s a končí časem t2 = 4 s. V čase t1 = 3 s má kámen rychlost 30 m/s a v čase t2 = 4 s má rychlost 40 m/s. Průměrná rychlost pak je 35 m/s a celková doba letu t = 1 sekunda, tedy uražená dráha je 35 m. Mohli bychom užít i vztah $s = v_0t + \frac{1}{2}gt^2 = 30\cdot 1 + 5\cdot 1^2 = 35\jm$.
e) Celková doba pádu je $t = \sqrt{\frac{2s}{g}} = 5,83\js$, tedy dopadová rychlost $v = gt = 58,3\jv$.
f) Rychlost 50 m/s bude mít v čase t = 5 s. Za tu dobu urazil dráhu $s=\frac{1}{2}gt^2 = \frac{1}{2} \cdot 10 \cdot 5^2 = 125\jm$ a bude tedy ve výšce 45 metrů nad zemí.
Erik hned na konci obce sešlápl plyn svého pekáče až k podlaze a se zrychlením 1,5 m/s2 zrychlil z 50 km/h na 90 km/h. Jakou vzdálenost mezitím ujel? Počítejte dvěma různými způsoby – jednak na základě průměrné rychlosti a jednak ze vztahu mezi dráhou a zrychlením.
Nejprve převedeme rychlosti z km/h na m/s.
Počáteční rychlost:
$v_0 = 50 \, \text{km/h} = \frac{50 \times 1000}{3600} \, \text{m/s} = 13,89 \, \text{m/s}$
Konečná rychlost:
$v = 90 \, \text{km/h} = \frac{90 \times 1000}{3600} \, \text{m/s} = 25 \, \text{m/s}$
Známe zrychlení $a = 1,5 \, \text{m/s}^2$ a chceme spočítat dráhu.
1. Výpočet na základě průměrné rychlosti
Průměrná rychlost je dána vztahem:
$v_{\text{prům}} = \frac{v_0 + v}{2}$
Zřejmě je to 70 km/h = 19,45 m/s.
Nyní vypočítáme čas, za který Erik dosáhne konečné rychlosti, podle vztahu:
$t = \frac{v – v_0}{a}$
Dosadíme hodnoty:
$t = \frac{25 \, \text{m/s} – 13,89 \, \text{m/s}}{1,5 \, \text{m/s}^2} = \frac{11,11 \, \text{m/s}}{1,5 \, \text{m/s}^2} = 7,41 \, \text{s}$
Dráha je potom dána vztahem:
$s = v_{\text{prům}} \times t$
$s = 19,45 \, \text{m/s} \times 7,41 \, \text{s} = 144,14 \, \text{m}$
2. Výpočet ze vztahu mezi dráhou a zrychlením
Použijeme rovnici pro dráhu při rovnoměrně zrychleném pohybu:
$s = v_0 t + \frac{1}{2}at^2$
Dosadíme hodnoty v základních jednotkách (čas jsme již spočetli v předešlé sekci):
$s = 13,89 \times 7,41 + 0,5 \times 1,5 \times 7,41^2 = 144 \, \text{m}$
Výsledná dráha, kterou Erik ujel, je přibližně $144 \, \text{m}$.
Auto může obecně zpomalovat se zrychlením maximálně a = -6 m/s2.
a) Jak dlouhá je brzdná dráha, pokud auto jede v obci rychlostí v0 = 50 km/h? Řešte nejprve obecně (jen pomocí písmen) a poté pro konkrétní zadané hodnoty.
b) Co kdyby auto jelo nepovolenou rychlostí 60 km/h? Jak se prodlouží brzdná dráha?
Nejprve řešíme obecně.
Doba, než auto zastaví, je
$ t = v_0/a$.
Průměrná rychlost během zastavování je polovina počáteční rychlosti: $v_p = v_0/2$.
Uražená dráha pak je $s = v_p t = v_0/2 \times v_0/a = \frac{v_0^2}{2a}$.
Dosadíme v základních jednotkách
$s = \frac{v_0^2}{2a} = \frac{13,89^2}{2 \cdot 6} = 16,1 \, \text{m}$.
Brzdná dráha při rychlosti $50 \, \text{km/h}$ je tedy přibližně $16,1 \, \text{m}$.
Všimněme si, že brzdná dráha závisí na druhé mocnině počáteční rychlosti. Pokud počáteční rychlost bude 60 km/h, tak vlastně platí, že $v’_0 = 1,2 v_0$. Pokud rychlost zvětšíme $1,2\times$, tak dráha se zvětší $(1,2)^2\times = 1,44 \times$, tedy o 44%, skoro o polovinu.
Vidíme, že i relativně malé překročení rychlosti vede k velkému prodloužení brzdné dráhy.
Těžký nákladní vlak s padesáti vagony gumových medvídků jel rychlostí 90 km/h, když strojvedoucí 300 metrů před sebou spatřil strom padlý přes trať. Okamžitě aktivoval brzdný systém, který je schopen brzdit se zrychlením 0,8 m/s2. Jakou rychlostí do stromu vlak narazil? Přežijí to medvídci?
Počáteční rychlost je 25 m/s.
Platí $s = v_0t – \frac{1}{2}at^2$. Neznámou v rovnici je čas. Dosadíme známé hodnoty: $300 = 25t – 0,4t^2$. To je kvadratická rovnice, kterou řešíme přes diskriminant nebo doplněním na čtverec. Výsledkem jsou dva kořeny pro čas, a sice 16,2 s a 46,3 s. Relevantní čas je jen ten první, protože druhý delší čas by odpovídal situaci, že vlak kmen přejede, poté někde dobrzdí do nuly a následně začne couvat, až znovu strom přejede.
Jelikož zpomalování trvá 16,2 s, tak výsledná rychlost bude v = 25 – 0,8*16,2 = 12,04 m/s = 43,3 km/h.
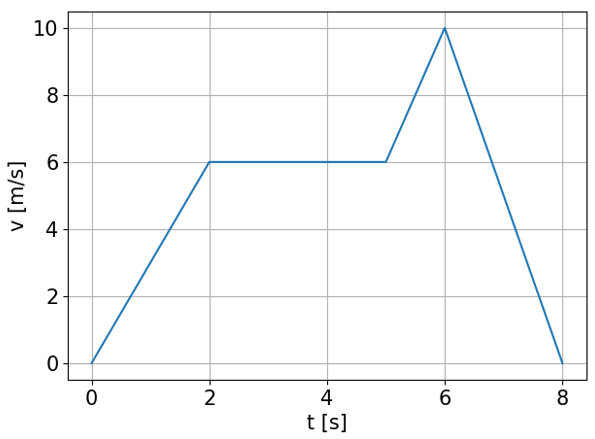
Výborný fotbalový útočník pan Jouda se při průniku do vápna pohyboval podle grafu rychlosti v(t) na obrázku výše. Určete co nejjednodušeji celkovou uraženou dráhu a zrychlení na jednotlivých úsecích.
Celková dráha odpovídá obsahu plochy pod křivkou. Sčítáním obsahu trojúhelníků a obdélníku dostaneme dráhu 42 metrů. Zrychlení jsou postupně 3, 0, 4 a -5 m/s2.
Vrhy
Svislý vrh
Zopakujme si volný pád. Helmut stojí na kraji propasti Machocha s hloubkou h = 138 m a neuvážlivě upustil chleba s máslem a salámem. Odpor vzduchu velkoryse zanedbáme.
a) Vyjádřete dobu letu $t$ a dopadovou rychlost $v$ obecně, tedy pro obecnou hloubku $h$.
b) Určete dobu letu a dopadovou rychlost pro zadaný případ propasti Macocha.
a) $h = \frac{1}{2}gt^2$, odtud vyjádříme čas:
$t = \sqrt{2h/g}$
a rychlost
$v = gt = g\sqrt{2h/g} = \sqrt{2hg}$.
Číselně doba letu je 5,3 s a rychlost dopadu 52 m/s. Nutno pozmamenat, že v realitě s odporem vzduchu bude doba letu delší a rychlost dopadu výrazně menší.
Brzdná dráha při rovnoměrně zpomaleném pohybu až do zastavení lze vyjádřit vztahem $s = \frac{1}{2} at^2$, tedy stejně jako dráha pro rovnoměrně zrychlený pohyb. Dokažte toto tvrzení.
První argument může být grafický. Při rovnoměrně zrychleném pohybu z nuly je plocha pod grafem $v(t)$ trojúhelník s obsahem právě $s = \frac{1}{2} at^2$. Při rovnoměrně zpomaleném pohybu do nuly je plocha pod $v(t)$ stejný trojúhelník, akorát zrcadlově převrácený. Jeho obsah tedy musí jít vyjádřit stejným způsobem.
Druhý argument může být početní. Dráha zpomaleného pohybu je
$s = v_0t – \frac{1}{2}at^2$
Avšak $v_0 = at$ a dosazením tohoto vyjádření do vztahu pro dráhu máme
$s = v_0t – \frac{1}{2}at^2 = at^2 – \frac{1}{2}at^2 = \frac{1}{2}at^2$.
Budeme se nyní zabývat svislým vrhem, tedy situací, kdy vyhodíte něco svisle nahoru, předmět dosáhne nejvyššího bodu a poté zase začne padat. Uvažujte g = 10 m/s2.
a) Pokud Ivánek vyhodí kyj svisle vzhůru rychlostí 20 m/s, za jak dlouho spadne na zem?
b) Jakou rychlostí spadne na zem?
c) Jak vysoko vystoupá?
d) Nakreslete graf rychlosti v(t) a výšky kyje h(t) v závislosti na čase.
a) Rychlost ubývá každou sekundu o 10 m/s2. Doba, než dosáhne nejvyššího (kulminačního) bodu je proto $t_k = v_0/g = 2\,\text{s}$. Poté kyj začne padat zase dolů. Situace při pádu je ale symetrická situaci při stoupání – pád je vlastně jakoby stoupání, kdy čas běží pozpátku. Doba pádu je tedy totožná jako doba stoupání a celková doba letu je $t = 2t_k = 4\,\text{s}$.
b) Vzhledem k symetrii mezi stoupáním a pádem bude i dopadová rychlost totožná jako rychlost výhozu, tedy 20 m/s.
c) Doba stoupání je 2 s a průměrná rychlost během stoupání je 10 m/s a zřejmě tedy vystoupá do výšky 20 m. Obecně to lze vyjádřit jako $h = \frac{v_0}{2}t = \frac{v^2_0}{2g}$. Mezi počáteční rychlostí a výškou výstupu platí stejný vztah jako mezi koncovou rychlostí a výškou pádu, což jsme již odvodili mnohokrát dříve: $v = \sqrt{2hg}$. Vyjádřením $h$ z tohoto vztahu dostaneme stejný výsledek.
d) Přenecháváme čtenáři.
Horáček a Pažout se hádají, kdo vyhodí výše ukradené utržené sluchátko. Pokud víme, že Horáček vyhodí sluchátko o 50% větší rychlostí, kolikrát výše sluchátko vystoupá?
V předchozí úloze jsme odvodili, že výška výstupu roste s druhou mocninou počáteční rychlosti (podobně jako to bylo u brzdné dráhy auta). Proto nárůst rychlosti faktorem $1,5\times$ bude znamenat 1,5^2\times = 2,25\times$ výšku výstupu.
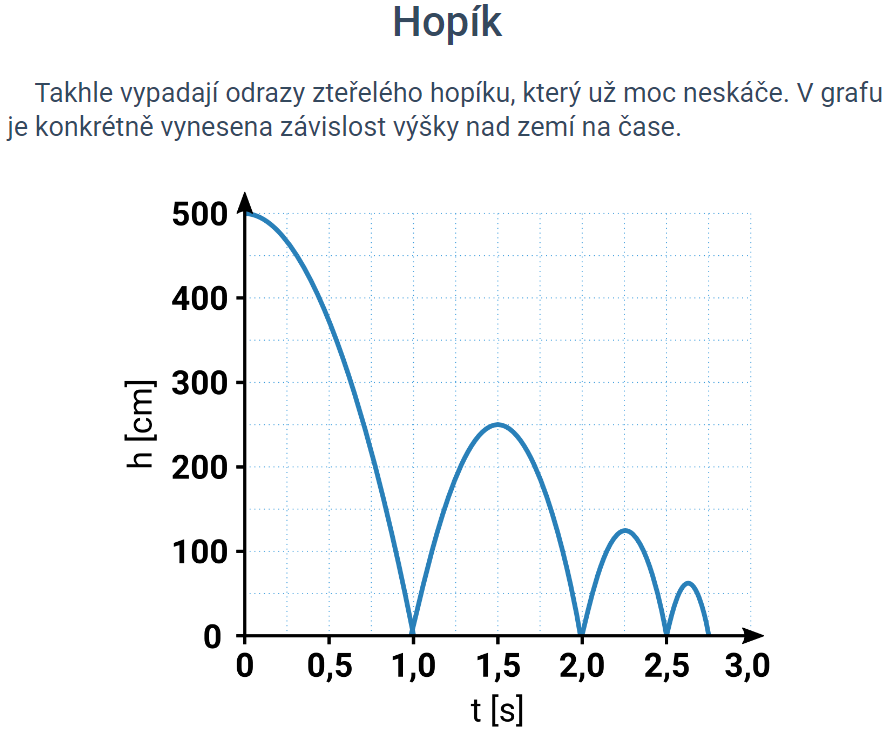
V jinak dobré internetové cvičebnici Umímeto je uveden obrázek výše, který má znázorňovat závislost výšky hopíku na čase, když se odráží od podlahy. Co je v obrázku špatně? Jak by obrázek měl vypadat správně? Na základě čeho si snadno můžeme všimnout, že je špatně?
Graf do prvního úderu o zem je v pořádku, pak již ale ne. Pokud hopík vystoupí do výše 250 cm, tak doba stoupání bude 0,71 s, nikoli 0,5 s. Podobně jsou nesprávně dlouhé doby skoků i ve zbytku grafu. Autor grafu předpokládá, že hopík v každém dalším skoku vyskočí do poloviční výšky než v předchozím, avšak není správná úvaha, že poloviční výška znamená poloviční čas. Správně by tedy druhý a další obloučky měly být roztaženější, než jak je nakresleno. Chybnost grafu vidíme taky z toho, že prudkost křivky při dopadech se zdá stále stejná, ne-li větší při pozdějších dopadech. To ale není možné, protože hopík pokaždé padá z menší výšky a dopadová rychlost tak musí být menší a tedy prudkost grafu v okolí dopadu bude postupně klesat.
Vodorovný vrh
Tomáš si chce vylít zlost, a proto si stoupnul na horní okraj lomu a mrštil svým mobilním telefonem vodorovným směrem do vody s počáteční rychlostí 18 m/s. Mobil po chvilce dopadl 45 m horizontálně před něj do vody. Odpor vzduchu zanedbáme, uvažujme g = 10 m/s2.
a) Jakou dobu mobil letěl?
b) Jak vysoko je okraj lomu nad hladinou?
c) Jakou velikost měla svislá složka dopadové rychlosti?
d) Jakou celkovou velikost měla dopadová rychlost a jaký svírala úhel s hladinou?
a) Horizontální složka rychlosti je neustále 18 m/s, tedy doba letu je $t = d/v_h = 2,5\,\text{s}$.
b) Hloubka pádu je $h = \frac{1}{2}gt^2 = 31,25\,\text{m}$.
c) Vertikální složka dopadové rychlosti zřejmě $v_v = gt = 25\,\text{m/s}$.
d) Celková dopadová rychlost z Pythagorovy věty $v = \sqrt{v^2_h + v^2_v} = 30,8\,\text{m/s}$. Pro úhel dopadu vůči hladině platí $\tan\alpha = v_v/v_h$, tedy $\alpha = \tan^{-1}(25/18) = 54°$.
Odvoďte vztah pro horizontální délku $d$ vodorovného vrhu při počáteční rychlosti $v_0$, výšce místa vrhu $h$ a gravitačním zrychlení $g$.
Doba pádu je jako pro volný pád, již dříve bylo odvozeno $t = \sqrt{2h/g}$. Horizontální délka je jednoduše $d = v_0 t = v_0 \sqrt{2h/g}$.
Martin se stal humanitárním letcem, který z letadla shazuje balíky plné čokolády. Letí ve výšce 200 m nad zemí rychlostí 60 m/s. Míří na matraci umístěnou na zemi. V jaké vzdálenosti před matrací musí balík vypustit?
Stačí si uvědomit, že se vlastně ptáme na délku vodorovného vrhu. Dosadíme do dříve odvozeného vztahu $d = v_0 \sqrt{2h/g}$ a dostaneme d = 380 m. To je skoro dvojnásobek výšky letu!
Šikmý vrh

Lionel Messi se chlubí, že překopne celé fotbalové hřiště. Vykopává od brány rychlostí $v_0$ = 126 km/h pod úhlem $\alpha$ = 30° vůči zemi, přičemž na stadionu předem radši odsáli veškerý vzduch. Překopne hřiště? Řešte nejprve obecně a pak pro konkrétní hodnoty.
a) V jaké vzdálenosti míč dopadne?
b) Jak vysoko míč vystoupá?
c) Jaká bude dopadová rychlost míče?
Nejprve převedeme rychlost z km/h na m/s: $v_0 = 35 \, \text{m/s}$
Úhel výkopu je $\alpha = 30^\circ$.
Rozložíme počáteční rychlost do horizontální a vertikální složky:
$v_{0x} = v_0 \cos \alpha = 30,3\,\text{m/s}$
$v_{0y} = v_0 \sin \alpha = 17,5\,\text{m/s}$
a) V jaké vzdálenosti míč dopadne?
Použijeme vztah pro dobu letu. Doba letu je dána tím, kdy míč dosáhne maximální výšky a následně se vrátí na zem. Čas výstupu do maximální výšky je dán vztahem:
$t_{\text{nahoru}} = \frac{v_{0y}}{g}$
Dosadíme hodnoty:
$t_{\text{nahoru}} = \frac{17,5 \, \text{m/s}}{9,81 \, \text{m/s}^2} \approx 1,78 \, \text{s}$
Celková doba letu je dvojnásobkem této hodnoty (čas nahoru i dolů):
$t_{\text{letu}} = 2 \times t_{\text{nahoru}} = 2 \times 1,7 \, \text{s} = 3,56 \, \text{s}$
Horizontální vzdálenost (délka, kterou míč překoná) je dána vztahem:
$d = v_{0x} \times t_{\text{letu}}$
Dosadíme hodnoty:
$d = 28,87 \, \text{m/s} \times 3,4 \, \text{s} \approx 108 \, \text{m}$
Míč dopadne přibližně $108 \, \text{m}$ od místa výkopu. To je zhruba jako délka fotbalového hřiště.
b) Jak vysoko míč vystoupá?
Maximální výška, které míč dosáhne, je dána vztahem:
$h_{\text{max}} = \frac{v_{0y}}{g}t = \frac{v_{0y}^2}{2g}$
Dosadíme hodnoty a získáme výšku 15,6 m.
c) Jaká bude dopadová rychlost míče?
Dopadová rychlost je úplně totožná jako rychlost výstřelu, protože horizontální složka rychlosti se nemění a vertikální složka se oproti výstřelu jen změnila na opačnou.
Pod jakým úhlem je potřeba vystřelit, aby střela dopadla co nejdál? Tedy pro danou počáteční rychlost se snažíme najít úhel výstřelu vůči zemi, aby byl dostřel maximální.
Vztah pro délku dostřelu jsme odvodili dříve:
$d = v_{0x}\cdot 2\t_k = v_{0x} \cdot 2 v_{0y}/g = v_0\cos\alpha \cdot 2 v_0\sin\alpha/g$. Ještě upravíme
$d = \frac{2v^2_0}\cos\alpha\sin\alpha}{g}$.
Pro jaký úhel $\alpha$ je tento výraz maximální? Všimneme si, že známe vztah pro sinus dvojnásobného úhlu $\sin2\alpha = 2\sin\alpha\cos\alpha.$ Výraz $\sin\alpha\cos\alpha$ proto nabývá maxima ve stejné chvíli, jako výraz $\sin2\alpha$. Sinus ale nabývá maxima zřejmě pokud jeho argument je 90°, tedy pokud $2\alpha = 90°$, proto $\alpha = 45°$.
Ideální úhel výstřelu je tedy 45°.
Na základě vztahu pro dvojnásobný úhel lze také přepsat délku vrhu jako
$d = \frac{v^2_0}{g}\sin2\alpha$, ze kterého je také vidět, že ideální úhel je 45°.
V jedné z řady dalších nesmyslných válek má neznámý vojín za úkol nastavit hlaveň granátometu tak, aby granát dopadl do vzdálenosti 400 m, přičemž ví, že úsťová rychlost výstřelu je 100 m/s. Pod jakým úhlem vůči svislému směru je třeba hlaveň nastavit? Řešte nejprve obecně.
Vyjdeme ze vztahu pro délku vrhu $d = \frac{v^2_0}{g}\sin2\alpha$ a vyjádříme úhel:
$\sin2\alpha = \frac{dg}{v^2_0}$, čili $\alpha = \frac{1}{2}\sin^{-1}(\frac{dg}{v^2_0})$.
Dosazením dostaneme $\alpha = 78,44°$. Toto je však úhel vůči vodorovnému směru.
Vůči svislici bude úhel roven $\beta = 12,56°$. To není velký odklon.
Dokažte, že trajektorií šikmého vrhu je parabola (při zanedbání odporu vzduchu). Tedy chceme ukázat, že body trajektorie $y(x)$ tvoří parabolu. Určete rovnici této paraboly.
Jedná se o složení rovnoměrného vodorovného pohybu a svislého rovnoměrně zpomaleného/zrychleného pohyub. Pro časové závislosti souřadnic platí:
$x(t) = v_{0x}\cdot t$ a $y(t) = v_{0y} t – \frac{1}{2}gt^2$.
Chceme $y(x)$, tedy z prvního vztahu vyjádříme čas a máme $t = x/v_{0x}$ a dosadíme do druhého vztahu
$y(x) = v_{0y} x/v_{0x} – \frac{1}{2}g(x/v_{0x})^2 = \frac{v_{0y}}{v_{0x}}x – \frac{g}{2v^2_{0x}}x^2$.
Zřejmě se tedy jedná o parabolu.
*Odvoďte vztah pro horizontální vzdálenost šikmého vrhu v případě, že střílíme z kopce, tedy ze svahu s úhlem $\beta$, přičemž úhel výstřelu $\alpha$ měříme vůči vodorovnému směru.
Necháme na čtenáři. Jedna z cest řešení může být, že použijeme analytické vyjádření křivky $y(x)$ získané v minulé úloze a budeme hledat její průsečík s přímkou “země”, tedy s přímkou s rovnicí $y = -\tan\beta\cdot x$. Vyjde nám souřadnice x průsečíku, což je právě hledaná horizontální vzdálenost.
Výsledek by měl být $d_x = \frac{(2v^2_0\cos^2\alpha)(\tan\alpha + \tan\beta}{g}$.
Tento výraz jde samozřejmě ještě různě upravovat při vědomí, že $\tan\alpha = \sin\alpha/\cos\alpha$.
Odvoďme vztah pro délku šikmého vrhu, když střílíme ze svahu s úhlem $\beta$, přičemž úhel výstřelu $\alpha$ je měřen vůči vodorovnému směru.
*Odvoďte vztah pro horizontální vzdálenost šikmého vrhu v případě, že střílíme sice na rovné zemi, ale z výšky h.
Necháváme na čtenáři.