Studenti budou měřit, jak závisí perioda T kmitání kyvadla na délce kyvadla. Poté se pokusí najít, jak tuto závislost vyjádřit matematicky. Zkusí touto závislostí nafitovat data. Následně vyvodí velikost gravitačního zrychlení. Pro SŠ, 60-90 min, vhodné spíš do semináře.
Pomůcky: provázek nastříhaný na kusy asi 120 cm dlouhé; zip sáčky pro umístění mobilu; mobilní telefon s internetem; nainstalovaná aplikace Phyphox. (Mobil jde ovládat skrz zip sáček a sám tedy tvoří “závaží” na závěsu. Phyphox samozřejmě není nutný, jde odměřovat periodu ocelového závaží úplně klasicky na stopkách a poté jen použít internetovou kalkulačku Desmos ke zpracování dat.)
Důležitou součástí je zpracování dat v grafické kalkulačce Desmos, která jde dobře použít i na mobilu. Zde si studenti vyzkouší proces “fitování dat”, kdy budou experimentálními body T(L) co nejpřesněji prokládat vhodnou matematickou funkcí. Fitování je denním chlebem všech experimentálních fyziků!
Před aktivitou: Ukážu kmitání kyvadla (závaží na provázku) a zavedu diskusi, na jakých parametrech a jakým způsobem bude záviset perioda kmitání kyvadla. Hrubě představím celý postup experimentu včetně zpracování dat k online kalkulačce Desmos. Také krátce pohovořím o akcelerometrech, což jsou sensory pohybu v mobilu.
Zadání
Úkolem bude změřit, jak závisí perioda T kmitání kyvadla na délce kyvadla. Poté se pokusíme najít, jak tuto závislost vyjádřit matematicky.
- Nainstalujte si na mobil aplikaci Phyphox. Tato aplikace umí komunikovat se sensory uvnitř mobilu (např. akcelerometry) a číst z nich data.
- Najděte si v aplikaci sekci “Kyvadlo”. Aplikace umí měřit periodu kmitu.
- Vložte svůj mobil do průhledného zip sáčku a přivažte k sáčku provázek o délce aspoň 1,2 m (obrázek)
- (Pokud nechcete k měření periody používat Phyphox, tak můžete na provázek zavěsit klasické závaží a pomocí mobilu stopovat dobu trvání např. 10 kmitů a z toho určovat periodu.)
Nejprve si vězměte fixní délku kyvadla (např. L = 1 m) a změřte periodu pro tři různě velké rozkmity a dvě různě těžká závaží.
Jak závisí perioda na velikosti rozkmitu?
Jak závisí perioda na hmotnosti závaží?
Nyní budeme měřit periodu v závislosti na délce kyvadla L. Délkou kyvadla zde rozumíme vzdálenost místa závěsu a těžiště mobilu, které se nachází přibližně v jeho středu. Počáteční rozkmit volíme spíše malý. Postupně nastavíme délky kyvadla např. na 30 cm, 45 cm, 60 cm, 90 cm a 120 cm a pro každou délku změříme periodu. Doplňte tabulku:
| L/m | T/s |
| 0,30 | |
| 0,45 | |
| 0,60 | |
| 0,90 | |
| 1,20 |
V dalším budeme kreslit grafy a vynášet délku na osu X a periodu na osu Y (Tedy L a x pro nás budou jedno a to samé, stejně jako T a y).
Najděte si na mobilu/tabletu aplikaci Desmos Graphing Calculator a vložte tabulku s naměřenými hodnotami. To provedeme tlačítkem “+” a vybereme “table”.
Rozhodněte, zda závislost periody na délce T(L) vypadá jako:
a) LINEÁRNÍ, b) KVADRATICKÁ, c) ODMOCNINNÁ
neboli a) $y=ax$, b) $y = Ax^2$, c) $y = A\sqrt{x}$
Své rozhodnutí zdůvodněte.
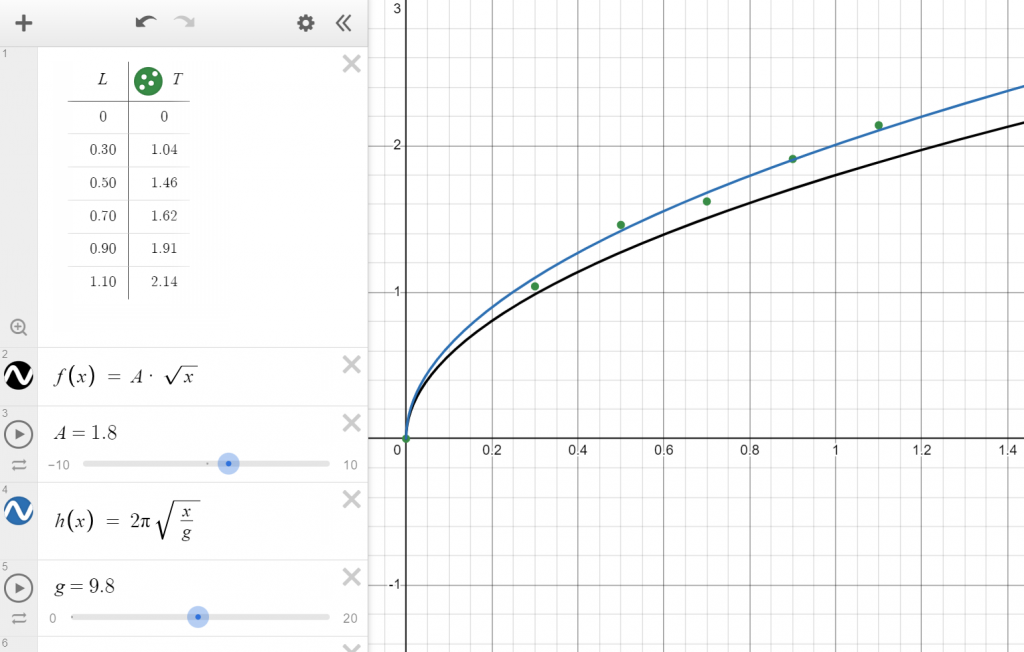
Na základě svého rozhodnutí do grafu vyneste jednu z těchto funkcí. Funkci vyneseme prostě zadáním předpisu např. $y(x) = Ax^2$ a potom zvolíme “add slider: A”. Nyní zvolte vhodnou hodnotu parametru A tak, aby funkce co nejlépe prokládala experimentální data (tomu se říká “nafitovat” data). Sledujte, zda tato funkce dobře odpovídá vašim datům. Pokud ne, zvolte jiný tvar funkce.
Zapište si hodnotu parametru A, která nejlépe prokládá data:
Vyhledejte si, jaký je skutečný předpis funkce, která vyjadřuje periodu kmitu v závislosti na délce kyvadla. Uvidíte, že ve funkci kromě délky L vystupuje hodnota gravitačního zrychlení g a pak už jen pár matematických konstant. Dokážete vyjádřit, co v této funkci odpovídá našemu parametru A, který jsme určili?
Ze znalosti parametru A vypočítejte velikost gravitačního zrychlení g!
Nápověda
Vztah pro periodu kyvadla je $T = 2\pi\sqrt{\frac{L}{g}} = A\sqrt{L}$. Proto platí $A = 2\pi/\sqrt{g}$. Odtud vyjádříme $g = (2\pi/A)^2$. Z hodnoty A tedy takto můžeme dopočítat hodnotu g.
Lepší fitování
Pokud by studenti měly problém s přechodem od A ke g, tak v pravý moment můžeme zjevit, že vztah pro periodu je $T = 2\pi\sqrt{\frac{L}{g}}$. Poté v Desmosu zavedeme přímo funkci ve tvaru $h(x) = 2\pi\sqrt{x/g}$. Přidáme slider pro parametr g a ladíme hodnotu g, aby křivka co nejlépe sedla na data.
Určete, pro jaký rozsah hodnot g křivka dobře sedne na data:
Ještě lepší automatické fitování
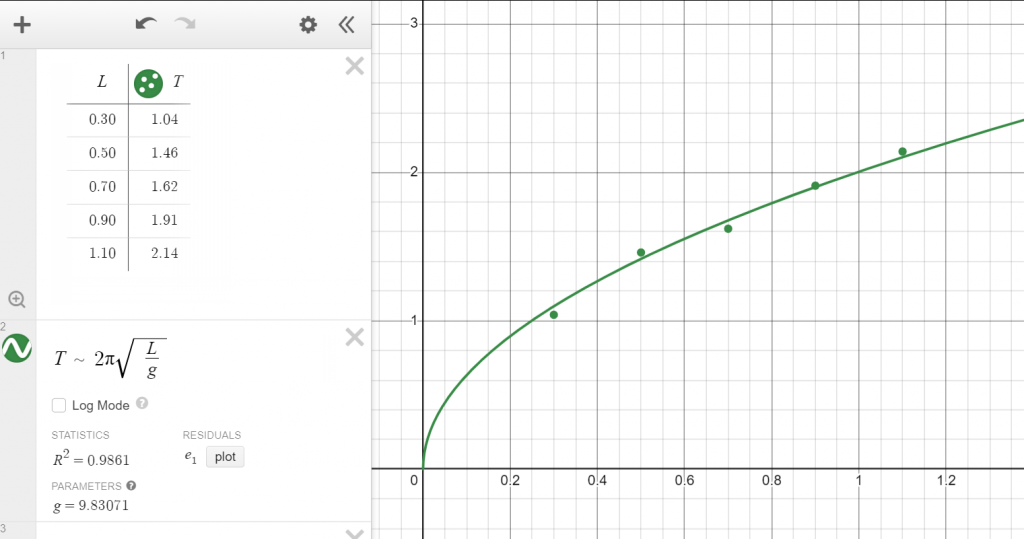
Vůbec nejsilnějším nástrojem pro fitování v Desmosu je ale automatické fitování pomocí metody nejmenších čtverců, kdy program sám najde nejlepší hodnoty parametrů, aby křivka pasovala co nejlépe na data. Pokud sloupce v tabulce pojmenujeme L, T, tak v Desmosu napíšeme $T \sim 2\pi\sqrt{L/g}$ a Desmos sám zobrazí nejlepší hodnotu g. Všimněte si, že nyní nepíšeme “=”, ale “~”! Pozor, pokud byl parametr g zaveden již v některé z předešlých funkcí, tak zde je potřeba ho pojmenovat jinak, třeba g1.
Zapište hodnotu g získanou automatickým fitováním a srovnejte s předchozími výsledky.
Pro chytré hlavy: Možná jsme celou dobu trochu špatně určovali délku kyvadla. Mohlo se stát, že tam byla třeba systematická chyba řekněme 0,5 cm plynoucí ze špatné znalosti polohy těžiště mobilu. Tedy že tato chyba byla ve všech měřeních stejná. Jak bychom mohli fitovací funkci pozměnit přidáním dalšího volného parametru, aby zohlednila možnou systematickou nepřesnost u určování délky?
Řešení
Mohli bychom použít funkci s dvěma volnými parametry A, b, třeba $y(x) = A\sqrt{x-b}$.
Diskutujte, z čeho mohou vyplývat nepřesnosti určení gravitační zrychlení. Vycházeli jsme že vztahu pro periodu matematického kyvadla. Byly však skutečně splněny předpoklady pro matematické kyvadlo? Jak bychom to mohli zařídit, aby předpoklady byly splněny co nejlépe?
Poznámky
- Nezapomeneme zmínit, že se ve skutečnosti nejedná o matematické kyvadlo, nýbrž o fyzikální (a co z toho plyne).
- Na závěr by měla proběhnout diskuse jednak o fyzice kyvadla, a jednak o zpracování dat. Je dobré se zeptat, s jakým krokem měli studenti nejvíce potíže.
- Určité potíže může činit ovládání webové aplikace Desmos Calculator. Učitel by si měl vše nejdříve vyzkoušet a seznámit se s rozhraním webové aplikace (např. jak změnit rozsah os, jak vložit datovou tabulku, jak změnit rozsah posuvníku atp.)
- Někteří studenti budou mít problém s formálním zápisem matematických vztahů a jejich přepsáním do Desmos. Také mohou být zmateni přechodem mezi prooměnnými L-x a T-y.
- Můžeme samozřejmě úplně ignorovat kalkulačku Desmos a místo toho použít třeba klasický Excel nebo Google Sheets, pokud na to mají studenti vhodná zařízení. Zpracování v Excelu dá maličko více práce než v Desmosu, ale zase si studenti procvičí práci v tabulkovém editoru, což je obecně užitečné.