
Ilustraci poločasu rozpadu s žetony a s pivem jsem v různých variantách viděla na webu mnohokrát z různých zdrojů (Jaderné hrátky, fyzikální šuplík nebo u pana Reichla). Nikde jsem ale nenašla protokoly rovnou vytisknutelné, tak sem naši verzi a způsob práce s pokusy dávám, třeba někdo využije. Naše verze (zatím ozkoušená v kvartě) pracuje s fazolemi, pivem a odměrnými válci. Počítače nevedeme v dostatečném množství, aby umožnily zapojení všech žáků tak, jak bych si představovala, proto jsme obešli “fitování exponenciály” tak trochu humpolácky.
Laboratorní práce s radioaktivními fazolemi: Použila jsem jako první seznámení s exponenciálou. Každá skupina dostala balíček 100 fazolí, které měly z jedné strany křížek a z druhé prázdnou stranu. (Nakřížkovat 700fazolí mi trvalo asi 20min) Fazole jsem zvolila proto, že čočka je příliš titěrná, a shánět 700mincí je pro peněženku příliš nešetrné. Jako rodič kvetu z večerních požadavků: Mami, potřebuju tohle a tohle, snažím se proto minimalizovat materiál, který si mají přinést žáci.
Jako první úkol měli žáci vyplnit tabulku, kam zaznamenávali počet “vrhů” a počet nerozpadlých fazolí. Začínáme na 0, se 100 nerozpadlými atomy – fazolemi, které zahrkáme v kelímku od jogurtu a vrhneme na lavici. Ty, které padly křížkem nahoru (rozpadlé atomy) dáme stranou a spočítáme ty, které padly prázdnou stranou nahoru (nerozpadlé atomy). S těmi pokus opakujeme, dokud se nám nerozpadnou všechny fazole. “Vrhací” část je za cca 10min hotová. Vše se zakreslí do grafu. Následně řešíme, jak to souvisí s radioaktivními atomy. Jaké by byly popisky os grafu, kdyby se nejednalo o fazole, ale radioaktivní atomy? (počet nerozpadlých atomů v procentech a čas – každý vrh reprezentuje uplynutí jednoho poločasu rozpadu).
Řešíme s žáky odpovědi na otázky pod grafem související s radiouhlíkovou metodou a snažíme se je navést na teoretický předpis exponenciály – v každé skupině to někdo vymyslel.

Celá laborka i s následnými otázkami vyšla na 45min, protokoly pro každého žáka tisknu 2 strany na A4 – ke stažení níže
Laboratorní práce poločas rozpadu pivních bublin: Potřebujeme odměrný válec (širší je lepší) či jinou válcovou nádobu pro každou skupinu, trochu piva, stopky na mobilu.
Bubliny časem praskají. Má tedy smysl určit jejich poločas rozpadu, tedy čas, za jak dlouho ve vzorku (pivní pěně) bude polovina bublin. Předpokládejme, že bubliny jsou stejně velké, plocha průřezu nádoby je také stále stejná v různých výškách. Když tloušťka pěny poklesne na polovinu, bude tedy poloviční i počet bublin.
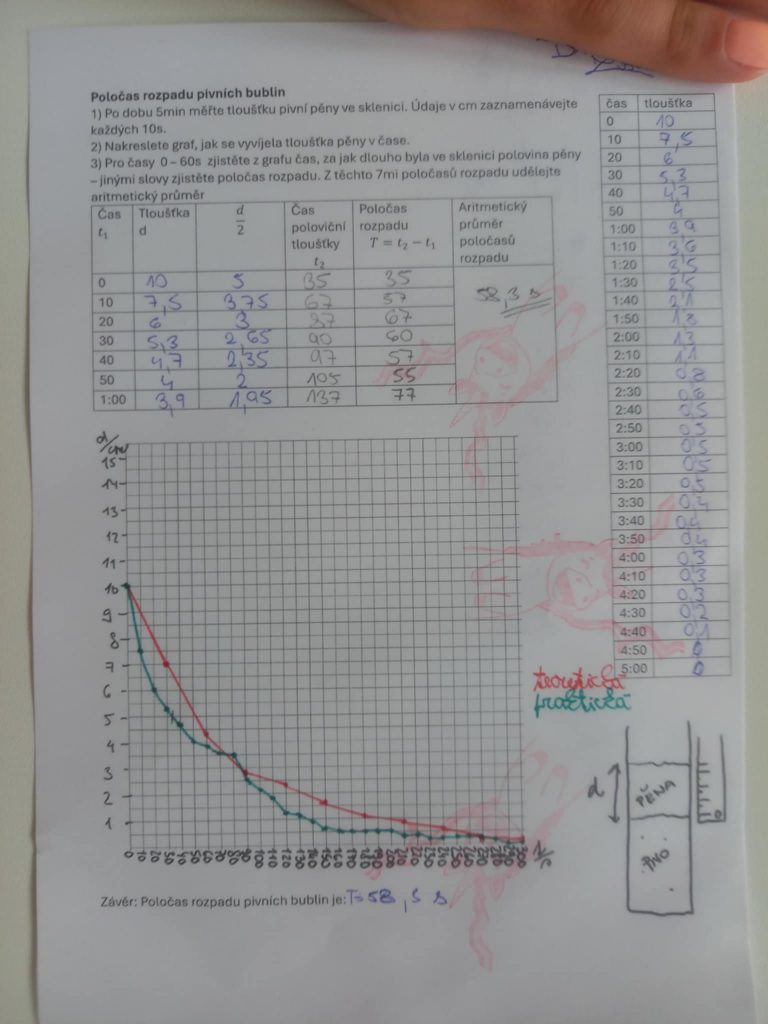
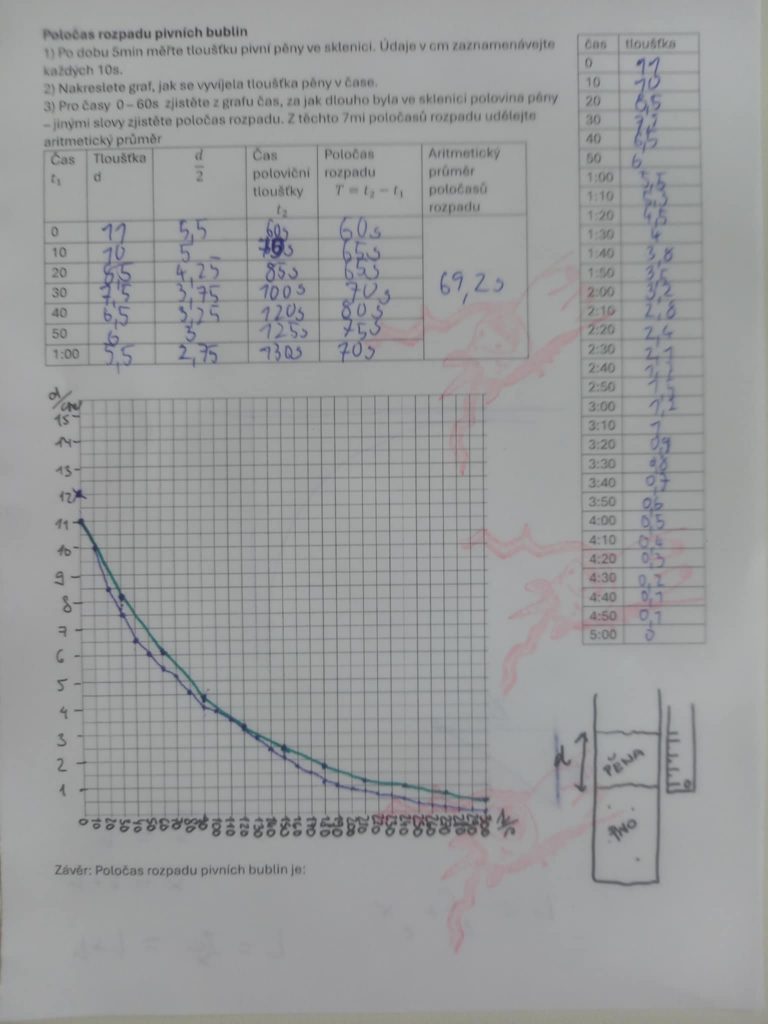
Hodnoty vyneseme do grafu. Pro časy 0 – 60s určíme, za jak dlouho od tohoto času t1 byla ve sklenici poloviční tloušťka pěny. Získáme tak 7 poločasů rozpadu a aritmetickým průměrem těchto 7mi časů získáme odhad, jaký zhruba poločas rozpadu pivních bublin je.
Celá laborka byla v kvartě na 45minut, pro 14 skupin mi stačily 2 pullitrové plechovky piva. (Zkoušela jsem pokus i s jarovou pěnou, ale má příliš velké bubliny) Většina skupin stihla všechny úkoly, některé skupiny nestihly dokreslení teoretické závislosti do grafu.

Na závěr přikládám odkazy na skvělé videa od Akademie věd ze série Nezkreslená věda, které jsme používali v hodinách jako podklad pro vypracování projektu na atomy a radioaktivitu (žáci dostali textové shrnutí, shlédli video a dostali seznam otázek, na které bych měla umět odpovědět, když se na jejich plakát o atomech a radioaktivitě podívám)
- Co je to atom
- Radioaktivita
- Jak funguje jaderná elektrárna (k tomuto videu přikládám výpisky a otázky, na které žáci hledali odpovědi)