- Elektrický náboj, Coulombův zákon
- Elektrické pole a jeho intenzita
- Vodiče a izolanty v elektrickém poli
- Napětí, práce, potenciál
- Kondenzátor, kapacita
Elektrický náboj, Coulombův zákon
Vyberte všechna správná tvrzení: Elementární náboj odpovídá
a) náboji elektronu; b) náboji 1 Coulomb; c) náboji protonu; d) náboji menšímu než 10-18 C; e) náboji alfa částice
Správně a, c, d.
Malinká kapička oleje byla ozářena rentgenovým zářením a poté bylo změřeno, že získala kladný náboj o velikosti 5,9 x 10-19 C, přičemž přesnost měření byla +- 20 %. Kolik elektronů kapička ztratila?
a) 5 nebo 6 elektronů
b) 3 nebo 4 elektrony
c) právě 4 elektrony
d) právě 2 elektrony
Elementární náboj je e = 1,6 x 10-19 C. Do požadovaného rozmezí se vejde 3-4 krát.
Správně b).
Základními jednotkami SI jsou m, s, kg, A, K, mol, cd. Vyjádřete jednotku Coulomb pomocí základních jednotek SI.
a) A.s; b) A.m/s; c) A/s; d) A.s/m
Správně a).
Na ocelovém háčku jsou zavěšeny dva lehké proužky alobalu. Tyčku nabijeme třením o hadr a přejedeme tyčkou po háčku. Vyberte pravdivá tvrzení.
a) na podobném principu pracuje zařízení zvané ampérmetr
b) proužky alobalu se k sobě přilepí
c) proužky alobalu se budou odpuzovat a vzdálí se
d) to, jestli se proužky budou k sobě přitahovat nebo odpuzovat, závisí na tom, jestli byla tyč nabita kladně nebo záporně
Správně c).
Vyberte události, ke kterým mohlo dojít v důsledku akumulace statického elektrického náboje třením a následnému přeskoku jiskry
a) požár na letišti při tankování paliva, když bylo zanedbáno uzemnění letadla a hadice
b) smrt muže na následky popálenin el. proudem po výběru nevhodných kalhot
c) vzplanutí vodíkové vzducholodi Hindenburg chvíli před přistáním
d) zničení citlivého mikroelektronického zařízení zaměstnancem, který si při manipulaci nenasadil uzemněný kovový náramek
Správně a, c, d.
Která z následujících zařízení silně využívají toho, že se drobné částečky nechají nabít a poté se přitáhnou k ploše nebo místu, které bylo nabito opačně?
a) při nanášení toneru na válec laserové tiskárny
b) při filtrování kouře od popílku např. v uhelných elektrárnách
c) v chladící věži jaderné elektrárny pro účinnější odvod aerosolu
d) v kvalitních reproduktorech pro vyčištění zvuku
Správně a, b.
Mějme dva stejné náboje nejdříve ve vakuu a poté ve skle. Ve kterém případě je síla mezi náboji větší?
a) ve skle; b) ve vakuu; c) je stejná
Pokud je rozdílná, tak kolikanásobně?
Sklo je dielektrikum, jeho relativní permitivita se pohybuje v rozmezí 5-10. Tímto faktorem se tedy síla mezi náboji zmenší (permitivita je v Coulombově zákonu ve jmenovateli).
Správně b): větší síla je ve vakuu, asi 5-10 násobně.
Určete velikost síly, kterou na sebe působí proton a elektron v atomu vodíku, pokud předpokládáme, že jsou od sebe ve vzdálenosti 0,5 nm. *Následně se zamyslete, jak velké zrychlení elektron v důsledku této síly zažívá. Jak je možné, že elektron “nespadne” do jádra?
a) 157 pN
b) 2,81 μN
c) 0,92 nN
d) 14,6 nN
Coulombův zákon pro sílu mezi bodovými náboji: $F = kQ_1Q_2/r^2$.
Dosadíme v základních jednotkách:
F = (9 x 10-9) · (1,6 x 10-19) · (1,6 x 10-19) / (5 x 10-10)2 = (9 x 1,62 / 25) · (10-9) = 0,92 · 10-9 N
Správně c) 0,92 nN.
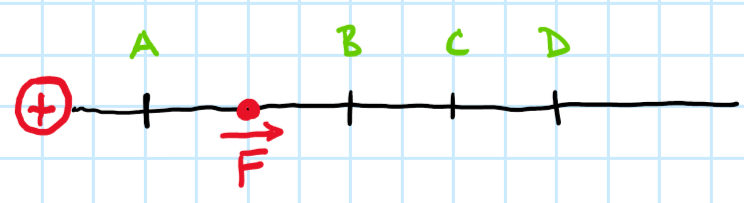
Na náboj ve vyznačeném bodě působí odpudivá síla o velikosti F. Určete velikost působící síly, pokud by se náboj nacházel v bodě A
a) 0,25 F
b) 0,5 F
c) 4 F
d) 1,5 F
e) 2 F
Správně c), 4F.
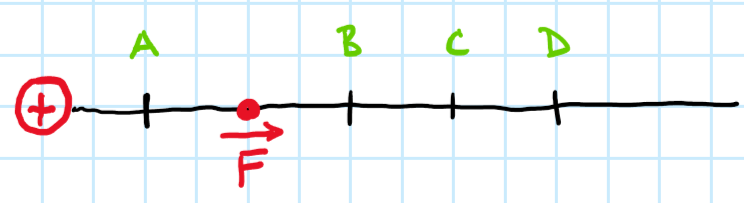
Na náboj ve vyznačeném bodě působí odpudivá síla o velikosti 100 mN. Určete velikost působící síly, pokud by se náboj nacházel v bodě D.
a) 16 mN
b) 500 mN
c) 50 mN
d) 25 mN
e) 200 mN
* Ve kterém bodě je síla přibližně poloviční, dvojnásobná, čtvrtinová?
Bod D je od kladného náboje ve 2,5-krát větší vzdálenosti a síla bude tedy 2,52 = 6,25-krát slabší, tedy asi 16 mN.
Poloviční je zhruba v bodě B, ale ne přesně. Dvojnásobné síle žádný vyznačený bod neodpovídá – je to mezi původním bodem a bodem A. Čtvrtinová síla v bodě C.
Správně a), 16 mN.
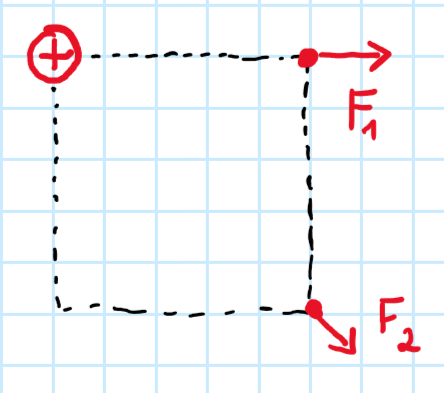
Pokud testovací náboj q umístíme do bodu 1, tak na něj působí síla F1 o velikosti 10 nN. Jak velká síla bude působit na testovací náboj, pokud ho umístíme do bodu 2? Napište v jednotce nN.
Vzdálenost bodu 1 od kladného náboje je 1 strana čtverce. Bod 2 má vzdálenost odpovídající úhlopříčce, tedy $\sqrt2$ strany čtverce. Síla pak je $(\sqrt2)^2$ = 2-krát menší, tedy 5 nN.
Síla v bodě 2 je 5 nN.
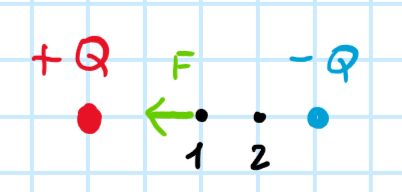
Mějme dva opačné náboje o velikosti Q. Mezi nimi je testovací náboj o velikosti q. Když je v bodě 1, tak na něj působí síla o velikosti 20 nN. Jakou velikost bude mít působící síla, když testovací náboj posuneme do bodu 2?
Ze směru naznačené síly plyne, že testovací náboj je záporný. V původní poloze tedy oba náboje na testovací náboj působí směrem doleva, každý silou 10 nN. Posunutím z bodu 1 do bodu 2 se testovací náboj přiblíží k zápornému na polovinu původní vzdálenosti (2x blíže), zatímco od kladného se vzdálí na 1,5 násobek původní vzdálenosti. Síla od záporného náboje tedy vzroste 4x, na 40 nN. Síla od kladného klesne 1,52 krát = 2,25 krát, tedy klesne na 10 nN / 2,25 = 4,44 nN. Výsledná síla v bodě 2 bude součtem těchto sil a bude mít velikost F2 = 44,44 nN.
Výsledná síla F2 = 44,44 nN.
Mezi dvěma bodovými náboji ve vakuu ve vzdálenosti d působí síla o velikosti F. Jaká bude velikost síly mezi dvěma stejně velkými náboji, když se vzdálenost čtyřikrát zmenší a náboje budou umístěny v plastu o relativní permitivitě εr = 3?
a) 12 F
b) 4F/3
c) 16F/3
d) 48F
Použijeme Coulombův zákon. Čtyřikrát bližší náboje znamená 42 = 16-krát větší síla. Relativní perimitivita vakua je 1, tedy v plastu je permitivita trojnásobná, což vede k 3x slabší síle.
Správně c), 16F/3.
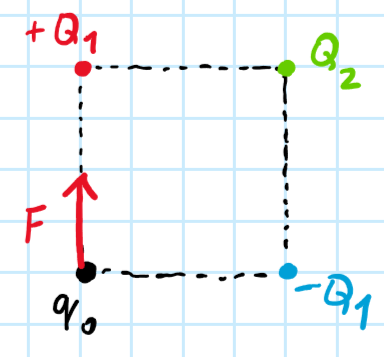
*V rozích čtverce máme postupně testovací náboj o velikosti q0, pak dva náboje o známé velikosti Q1 opačného znaménka, a konečně náboj o neznámé velikosti Q2. Víme, že na náboj q0 působí elektrická síla F ve vyznačeném směru. Jakou velikost a znaménko má náboj Q2?
a) 2Q1
b) -0,5 Q1
c) -Q1
d) 2,82 Q1
Kreslete si postupně síly na testovací náboj od jednotlivých nábojů. Kladný náboj velikosti Q1 musí přitahovat testovací náboj silou F1 směrem nahoru. Záporný náboj ho pak odpuzuje stejně velkou silou směrem doleva. Testovací náboj je tedy záporný. Výslednice těchto sil F11 pak působí směrem doleva nahoru a má velikost $\sqrt2$F1. Aby celková výsledná síla působila nahoru, tak náboj Q2 musí působit silou F2 směrem doprava nahoru, a tato síla musí mít stejnou velikost jako F11, tedy $\sqrt2$F1. Náboj Q2 je však přes úhlopříčku čtverce a v důsledku větší vzdálenosti je jeho silové působení poloviční. Aby i přes tuto větší vzdálenost bylo dosaženo větší síly, tak náboj Q2 musí být větší než Q1, a musí platit Q2 = 2$\sqrt2$Q1.
Správně d).
Elektrické pole a jeho intenzita
Na náboj o velikosti 0,2 μC působí elektrostatická síla o velikosti 600 nN. Určete intenzitu elektrického pole v daném místě v jednotce N/C.
E = Fe / q = (600 × 10-9 N) / (0,2 × 10-6 C) = 3 N/C.
Určete velikost síly, která působí na náboj o velikosti 5 mC v elektrickém poli o intenzitě 2000 N/C
Fe = qE = (5 × 10-3 C) · (2 × 103 N/C) = 10 N.
Napište heslo, které vznikne spojením následujících značek: veličina náboj, veličina intenzita elektrického pole, veličina síla, jednotka náboj náboj. Uveďte bez mezer vše velkými písmeny.
QEFC.
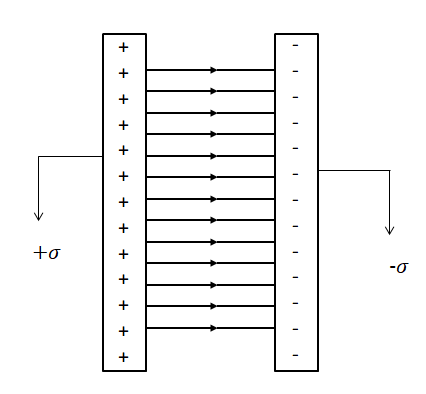
Mezi opačně nabitými rovnoběžnými deskami, které jsou blízko u sebe, najdeme
a) radiální pole
b) pole dipólu
c) homogenní pole
Homogenní pole c).
Rozhodněte, zda je pravdivé tvrzení: Mezi blízkými opačně nabitými rovnoběžnými deskami je elektrické pole u jedné z desek výrazně silnější, než elektrické pole na půli cesty mezi deskami.
a) ne
b) ano
Ne a) – homogenní pole má všude stejnou intenzitu.
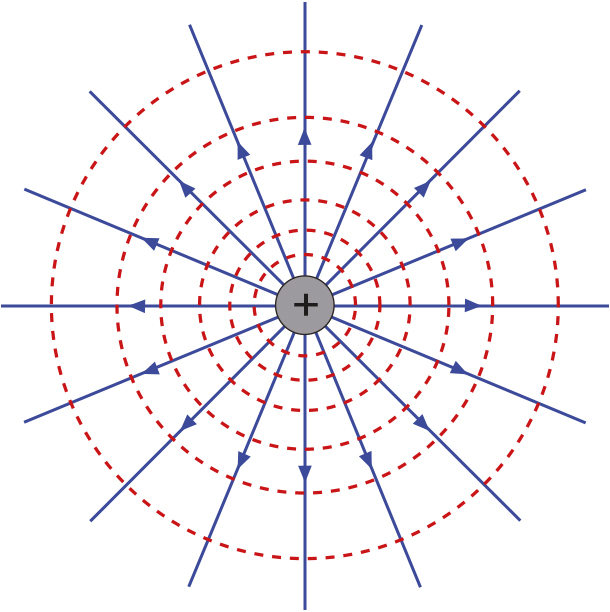
Pole na obrázku nazveme
a) bodové
b) radiální
c) kruhové
d) homogenní
Radiální pole b).
Mějme pole jako na obrázku výše. Pokud se vzdálíme od centrálního náboje na trojnásobek původní vzdálenosti, tak elektrická intenzita
a) klesne 9x
b) vzroste 9x
c) vzroste 3x
d) klesne 3x
e) nezmění se
Klesne 9x, a). Podle Coulombova zákona se intenzita mění s převrácenou druhou mocninou vzdálenosti.
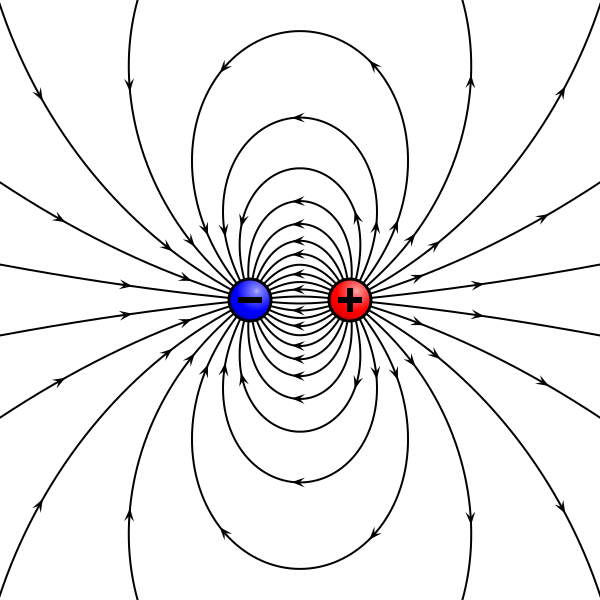
Mějme uspořádání náboje jako na obrázku. Rozhodněte, zda je velikost elektrického pole v prostoru popsána vztahem $E = kQ/r^2$, kde r je vzdálenost od středu spojnice kladného a záporného náboje. Zdůvodněte.
a) ano; b) ne
Ne, vztah nelze použít – platí jen pro pole jednoho bodového náboje.
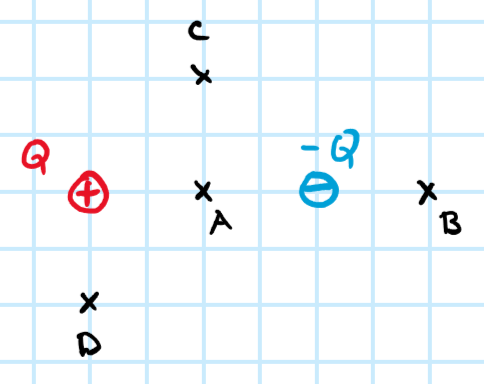
Pokud by v prostoru byl jen kladný náboj Q, tak by v bodě A byla intenzita elektrického pole o velikosti 100 N/C. Pak ale přidáme záporný náboj o velikosti Q. Určete velikost a směr intenzity el. pole v bodě C.
a) 71 N/C
b) 106 N/C.
c) 43 N/C
d) 27 N/C
*Dále určete intenzitu v bodě B a konečně D.
Vzdálenost bodu C od kladného náboje je $\sqrt{2}$-krát větší než vzdálenost bodu A od kladného náboje (vzpomeň na délku úhlopříčky čtverce). Intenzita od kladného náboje proto bude ${\sqrt2}^2$ = 2-krát menší, tedy 50 N/C. Stejně tak intenzita od záporného náboje. Avšak v bodě C nejdou intenzity od kladného a záporného náboje stejným ani opačným směrem (nakreslete si obrázek, kde intenzity znázorníte vektory). Platí ale, že vertikální složky vektorů intenzity se vyruší, zatímco horizontální složky se sečtou. Horizontální složka intenzity od kladného náboje má velikost cos(45°)$\cdot$50 N/C = 50/$\sqrt2$ = 35,36 N/C, stejně tak od záporného náboje. Výsledná intenzita má tedy horizontální směr a velikost 70,71 N/C.
Výsledná intenzita směr horizontálně doprava, velikost 70,71 N/C, možnost a).
Určete velikost síly působící na jádro hélia (alfa-částici), pokud se nachází v elektrickém poli o intenzitě 100 kN/C
a) 10-8 N
b) 3,2 x 10-14 N
c) 1,6 x 10-12 N
d) 100 kN
Alfa částice obsahuje dva protony a dva neutrony, její náboj je dvojnásobek elementárního, tedy q = 3,2 x 10-19 C.
F = qE = (3,2 x 10-19 C) · (105 N/C) = 3,2 x 10-14 N
Správně b) 3,2 x 10-14 N.
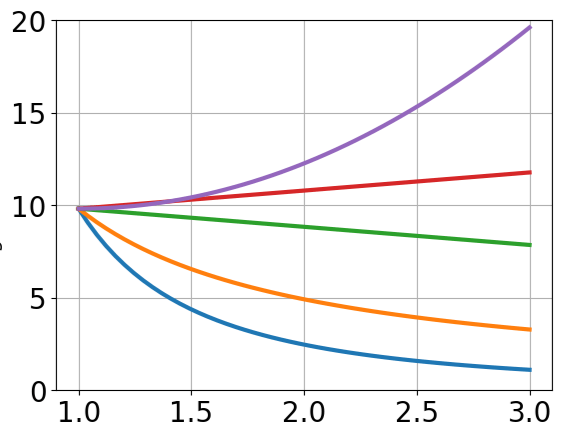
Graf znázorňuje závislost elektrické intenzity (N/C) na vzdálenosti (mm) od bodového elektrického náboje. Která z křivek zobrazuje závislost velikosti elektrické intenzity správně?
a) červená (2. shora)
b) fialová (1. shora)
c) oranžová (4. shora)
d) modrá (5. shora)
e) zelená (3. shora)
Ve dvojnásobné vzdálenosti musí být intenzita 4x menší. To platí pro nejspodnější křivku.
Správně d), modrá křivka.

Mějme dva bodové elektrické náboje o velikostech Q1 a Q2 ve vzájemné vzdálenosti 6 cm. Na přímce proložené těmito dvěma náboji bude existovat jedno či více míst, kde bude intenzita elektrického pole nulová. Kde budou tato místa nulové intenzity, pokud
a) Q2 = Q1
b) Q2 = -Q1
c) Q2 = 4Q1
d) Q2 = -4Q1
e) Q2 = -2Q1
a) Nulová intezita je uprostřed mezi náboji
b) Na přímce není žádné místo s nulovou intenzitou (leda v nekonečnu).
c) Nulová intenzita je mezi náboji v takovém místě, že poměr vzdálenosti k většímu náboji (2) a k menšímu náboji (1) je 2:1. Tedy toto místo leží 2 cm od menšího náboje (1) a 4 cm od většího náboje (2).
d) Místo nulové intenzity musí ležet nalevo od menšího náboje (1) tak, že poměr vzdálenosti k většímu náboji (2) a k menšímu náboji (1) je 2:1. Tedy toto místo leží 6 cm nalevo od náboje (1) a 12 cm nalevo od náboje (2).
e) Místo nulové intenzity musí ležet nalevo od menšího náboje (1) tak, že poměr vzdálenosti k většímu náboji (2) a k menšímu náboji (1) je $\sqrt2$:1. Vzdálenost k náboji (1) označme x.
Pak platí (x+6) : x = $\sqrt2$ : 1 = $\sqrt2$.
Tedy x+6 = $\sqrt2$x, neboli x = 6/($\sqrt2$ – 1) = 14,5 cm nalevo od náboje (1).
*Malá polystyrenová kulička hmotnosti m visí svisle na provázku. Poté ji vložíme do homogenního elektrického pole o velikosti E a kulička na provázku se od svislice odchýlí o úhel $\alpha$. Vyjádřete obecně velikost náboje kuličky q na základě ostatních veličin.
Po vychýlení provázek míří ve směru výslednice tíhové síly Fg = mg na kuličku a elektrostatické síly Fe = qE. Tyto síly jsou na sebe kolmé a tvoří tak odvěsny pravoúhlého trojúhelníku.
Pro úhel vychýlení pak platí tg(α) = qE / mg.
Odtud q = tg(α)mg/E.
*Alfačástice vlétá vodorovným směrem rychlostí v mezi svislé opačně nabité desky, které jsou ve vzájemné vzdálenosti d, je na ně přivedeno napětí U a mají délku L. Po průletu mezi deskami se směr částice odchýlil o úhel α od vodorovného směru. Vyjádřete počáteční rychlost částice v. Jaké další údaje kromě zadaných ještě bude potřeba znát? Ještě před výpočtem rozhodněte, zda při zvětšení dané veličiny bude vycházet rychlost větší či menší.
Při vlétnutí mezi desky začne na částici působit síla ve vertikálním směru. Vodorovná složka rychlosti částice se nemění, ale vertikální složka postupně narůstá. Alfačástice obsahuje dva protony a dva neutrony, tedy její náboj je q = 2e.
Síla na částici mezi deskami pak je F = qE = 2eU/d.
Vertikální zrychlení částice je a = F / m = 2eU / dm.
Doba průletu mezi deskami je t = L/v.
Při tom získá částice vertikální rychlost o velikosti u = at = aL/v.
Pro úhel odchýlení platí tg(α) = u/v.
Nyní již lze postupně vyjadřovat počáteční rychlost v:
$v = tg(\alpha)u = \frac{tg(\alpha)aL}{v} = \frac{tg(\alpha)2eUL}{vdm}$.
Proto
$v = \sqrt{\frac{tg(\alpha)2eUL}{dm}}$.
Vodiče a izolanty v elektrickém poli
Mezi opačně nabité desky, mezi nimiž je intenzita el. pole 1 kV/m, dáme plastovou PVC kostičku. Intenzita el. pole uvnitř kostičky bude
a) 3 kV/m
b) asi 0,25 kV/m
c) asi 0,9 kV/m
d) nulová
Relativní permitivita PVC je rovna asi 4, tedy pole se 4x zeslabí.
Správně b), intenzita asi 0,25 kV/m.
Mezi opačně nabité desky, mezi nimiž je intenzita el. pole 1 kV/m, dáme měďenou kostičku, uvnitř níž je dutina. V dutině bude intenzita el. pole
a) okolo 0,5 kV/m
b) 1 kV/m
c) nulová
Ve vodiči dojde k elektrostatické indukci, přesunutí volných nábojů a pole uvnitř vodiče bude nulové (pokud by pole bylo nenulové, tak se náboj dále bude přesouvat).
Správně c) – nulová.
Vysvětlete pojmy elektrostatická indukce a polarizace dielektrika, uveďte příklady.
Viz video a otázky níže.
Nejdříve otřeme plastovou tyč kůží. Poté položíme hliníkovou plechovku na stůl a přiblížíme k ní plastovou tyčku, aniž by se dotkly. Vyberte pravdivá tvrzení.
a) plechovka se začne odpuzovat od tyčky.
b) volné elektrony v plechovce se do určité míry přesunou na tu stranu plechovky blíže k tyčce.
c) Přitahování plechovky k tyčce je primárně způsobeno jevem polarizace dielektrika
d) Tyčka a plechovka na sebe silově působí, jedině když je tyčka elektricky nabitá. Potom se vzájemně přitahují.
Správně b, d.
Když třeme plastové brčko o triko, tak je pak možné ho přiložit třeba na stěnu nebo na dveře, a ono tam drží (“lepí”). Vyberte pravdivá tvrzení.
a) Brčko je elektricky neutrální
b) Ve stěně dojde k jevu polarizace dielektrika, kdy na ploše stěny dojde ke zorientování dipólů
c) Ve stěně se zorientují dipóly tak, že pokud je brčko kladně nabité, tak se záporné části dipólů co nejvíc přiblíží brčku.
d) Mezi stěnou a brčkem tekl kladný náboj a brčko se téměř okamžitě stalo elektricky neutrální.
Správně b, c.
Pro přenos internetu se používá kabel pojemnovaný STP (Shielded Twisted Pair). Vyberte správná tvrzení.
a) Datové kabely, zvlášť ty nestíněné, by se NEměly dávat příliš blízko k silovému kabelu vedoucímu do zásuvky.
b) Vodiče přenášející informace jsou umístěny do velmi tvrdé neprůhledné trubičky.
c) účelem je pomocí efektu Faradayovy klece zabránit rušení datového toku okolním elektrickým polem
d) Vodiče přenášející informace jsou opleteny kovovým rukávkem.
Správně a, c, d.
Co se bude dít, když třením o kůži nabijeme PVC trubku a přiblížíme k pramínku vody z kohoutku? Proč se to bude dít?
Pramínek vody se ohne, bude se přitahovat k trubce. Molekuly vody mají na jedné straně (atom kyslíku) převahu záporného náboje a na druhé straně (atomy vodíku) převahu kladného náboje. Molekula se chová jako elektrický dipól. Dochází k jevu polarizace dielektrika a tedy působení elektrické síly od nabité tyče na úhrnně neutrální vodu.
Napětí, práce, potenciál
Pepíček spojil póly zdroje napětí rezistorem. Když skrz rezistor protekl náboj o velikosti 4 C, tak elektrické práce vykonaly práci o velikosti 20 J, která se v rezistoru uvolnila ve formě tepla. Jaké napětí má zdroj?
W = QU, tedy U = W/Q = (20 J) / (4 C) = 5 V.
Zdroj má napětí 5 V.
Mějme dvě rovnoběžné velké desky blízko u sebe ve vzdálenosti d, nabité na napětí U. Pro velikosti elektrické intenzity pak platí
a) E = d/U
b) E = U.d
c) E = U/d
d) E = U2 · d
Správně c) E = U/d.
Kterými z následujících jednotek je možné vyjádřit intenzitu elektrického pole?
a) N·C
b) V/m
c) N/C
Správně b, c. Lze N/C nebo V/m.
Dvě paralelní kovové desky ve vzdálenosti 2 mm jsou připojeny na plochou 4,5 V baterii. Jak velkou práci vykonají elektrické síly při přenesení náboje o velikosti 400 mC z jedné desky na druhou? Uveďte v jednotce Joule.
Údaj o vzdálenosti desek je zde nadbytečný. Počítáme W = QU = (0,4 C) · (4,5 V) = 1,8 J.
Vykonají práci 1,8 J.
Mějme dvě rovnoběžné opačně nabité desky ve vzdálenosti d, mezi nimiž je napětí U a intenzita el. pole E. Ke kladné desce umístíme kladný testovací náboj q, na nějž působí elektrická síla F. Při přenesení náboje na zápornou desku vykoná elektrický síla práci W. Určete, které z následujících vztahů dávají smysl.
a) W = Ud
b) F = qE
c) U = Fd
d) E = U/d
e) W = qU
Správně b, d, e.
Jakou velikost má intenzita elektrického pole mezi rovnoběžnými kovovými deskami, které jsou ve vzdálenosti půl centimetru a připojené k pólům 12 V baterie? Vyjádřete v obou obvyklých jednotkách.
E = U/d = (12 V) / (0,5 x 10-2 m) = 2400 V/m = 2400 N/C.
Intenzita 2400 V/m = 2400 N/C
V suchém čistém vzduchu dojde k elektrickému průrazu (vzniku elektrického výboje), když intenzita el. pole přesáhne hodnotu 30 kV/cm. V jaké vzdálenosti by musely být rovnoběžné desky, aby došlo k překročení prahové intenzity, když mezi deskami bude napětí 600 V?
E = U/d, tedy d = U/E = (600 V) / (30000 V/cm) = 0,02 cm = 0,2 mm.
Vzdálenost 0,2 mm.
Kondenzátor, kapacita
Máme dva kondenzátory obashující stejně velký náboj. První z nich má menší kapacitu a druhý z nich má větší kapacitu. Na kterém naměříme větší napětí?
a) na druhém
b) na prvním
c) na obou stejné
Správně b) – větší napětí bude na kondenzátoru s menší kapacitou.
Které z následujících vztahů mezi napětím na kondenzátoru, náboji na desce a kapacitou kondenzátoru dávají smysl
a) U = QC
b) Q = CU
c) U = Q/C
d) C = Q/U
Správně b, c, d.
Jakou velikost má náboj na kondenzátoru o kapacitě 2200 μF nabitý na napětí 6 V? Uveďte v jednotce mC.
Q = CU = (2,2 × 10-3 F) · (6 V) = 13,2 mC.
Náboj 13,2 mC.
Mějme deskový kondenzátor. Co se stane s jeho kapacitou, když desky dáme do menší vzájemné vzdálenosti?
a)nezmění se
b)zmenší se
c)zvětší se
Správně c) – zvětší se.
Jak se v praxi docílí toho, aby i relativně malý kondenzátor měl slušně velkou kapacitu? Uveďte pokud možno co nejvíce cest. Existují nějaké limity?
Desky velice blízko u sebe – tenká vrstva izolantu může vzniknout např. elektrolytickou oxidací hliníkové elektrody. Velký povrch – svinutí elektrod do ruličky, případně elektroda také může mít mikrostrukturu s mnoha hrbolky a dutinami. Dielektrikum o vysoké permitivitě.
Proč nejde kapacitu kondenzátoru neustále zvětšovat tak, že budeme zmenšovat vzdálenost desek – řekněme na 10 nm, 1 nm, 0.1 nm, …?
Když izolační vrstva dielektrika bude příliš tenká, už nedokáže odizolovat napětí mezi deskami – pak by došlo k průchodu elektrického proudu mezi deskami a tedy “propálení” kondenzátoru.
Větší kapacity kondenzátoru je možné dosáhnout
a) vložením dielektrika s vyšší permitivitou
b) zvýšením napětí mezi deskami
c) oddálením desek
d) zvětšením plochy desek
Správně a, d.
Mějme kondenzátor o kapacitě C nabitý na napětí U nábojem Q. Kondenzátor pak postupně vybíjíme přes LED. Označte všechna pravdivá tvrzení.
a) Napětí na kondenzátoru zůstává prakticky konstantní.
b) Kapacita kondenzátoru klesá.
c) Napětí na kondenzátoru postupně klesá.
d) Celková energie dodaná do obvodu je E=QU.
Správně c).
Mějme dvě rovnoběžné desky kondenzátoru ve vzdálenosti 1 mm, mezi nimiž je vzduch. Jaká by musela být plocha desky, aby měl kondenzátor kapacitu 1 mF, tedy jako běžný školní kondenzátor?
a) 1652 m2
b) 113 tisíc m2
c) 80,9 m2
d) 0,64 m2
Vztah pro kapacitu deskového kondenzátoru: $C = \varepsilon_0 S/d$.
Odtud
$S = Cd/\varepsilon_0$ (pro vzduch bereme permitivitu vakua $\varepsilon_0 = 8,854 \times 10^{-12}$ F/m).
Dosadíme: S = (10-3 F) · (10-3 m) / (8,854 x 10-12 F/m) = 106/8,854 m2 = 113 tisíc m2
To je překvapivě hodně a kondenzátory použitelné v praxi je tedy potřeba dělat nějak chytřeji.
Margaret Thatcherová nabila kondenzátor na napětí 4 V. Na jaké napětí by ho musela nabít, aby byla energie kondenzátoru trojnásobná?
a) 6,9 V
b) 12 V
c) 9,4 V
d) 7,8 V
Pro energii kondenzátoru platí E = ½ CU2 , tedy energie roste s druhou mocninou napětí. Aby se energie zvýšila 3x, tak se napětí musí zvýšit $\sqrt3$ – krát, tedy ze 4 V na 6,9 V.
Na napětí 6,9 V.

Kondenzátor defibrilátoru má dodat energii 250 J při počátečním napětí 2000 V. Jaká musí být kapacita kondenzátoru?
a) 15 μF
b) 50 μF
c) 200 μF
d) 125 μF
Pro energii kondenzátoru platí E = ½ CU2 . Vyjádříme C = 2E/U2 = (500 J) / (4 ×106 F2) = 125 × 10-6 F.
Správně d), 125 μF.

Když seřadíme uvedená spojení stejných kondenzátorů podle kapacity od nejmenší, dostaneme
a) BAC
b) CBA
c) ABC
d) CAB
Správně CAB.
Pepíček má dva totožné kondenzátory. Nejprve je spojil sériově a změřil kapacitu Cs. Poté je zapojil paralelně a změřil kapacitu Cp. Jaký je podíl čísel Cs/Cp?
a) 4
b) 2
c) 0,5
d) 0,25
Paralelní spojení má dvojnásobnou kapacitu, sériově poloviční. Sériově má tedy čtvrtinovou kapacitu oproti paralelnímu. Cs, Cp
Poměr Cs/Cp = 0,25.
Helmut spojil sériově kondenzátory o kapacitách 1 mF, 2 mF a 3 mF a připojil k 6 V baterii.
a) Na kterém kondenzátoru je shromážděn největší náboj?
b) Na kterém kondenzátoru naměří největší napětí?
c) Jak by se změnila odpověď, kdyby kondenzátory byly spojeny paralelně?
a) Při sériovém spojení je na všech kondenzátorech stejný náboj.
b) Náboj je stejný a platí U = Q/C, tedy největší napětí bude na kondenzátoru s nejnižší kapacitou.
c) Při paralelním spojení bude na všech stejné napětí. Jelikož Q = CU, náboj bude největší na kondenzátoru s největší kapacitou.
Uveďte několik využití kondenzátoru.
Blesk fotoaparátu, defibrilátor, krátkodobé skladiště elektrické energie, elektronika, ladicí oscilační obvod, pro uchování informace v určitých typech počítačových pamětí, senzory a řada dalších.