Vítejte! V této kapitole se budeme bavit zejména o tom, jak síly ovlivňují pohyb těles. Představíme si všechny tři Newtonovy zákony, souvislost síly a zrychlení, pochopíme třecí sílu a pohyb po nakloněné rovině. Potom se budeme zabývat hybností a zákonitostmi srážek dvou těles, odkud vyplyne velmi významný zákon zachování hybnosti.
Kapitoly Tření a Nakloněná rovina máte možnost projít buď zrychleně jen pomocí shrnujícího videa, nebo podrobněji a pomaleji.
První a druhý Newtonův zákon
Tření
videa podrobněji a pomaleji:
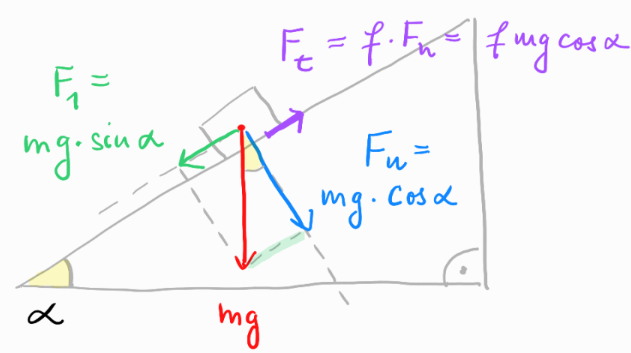
Nakloněná rovina
Podrobněji a pomaleji
Zákon akce a reakce, hybnost, zákon zachování hybnosti
motivační video youtube: Gun handling fails – backfire (zpětný ráz).
Shrnutí
video (yt) – dva složitější příklady z dynamiky
Poznámka: Pokud síla nepůsobí rovnoběžně s rychlostí tělesa, tak způsobuje změnu směru pohybu. Dostředivé síle se však budeme věnovat v některé z příštích kapitol.
Shrnutí a vztahy
$\newcommand{\ve}[1]{\boldsymbol{\mathit{#1}}}$
- Newtonův první zákon (zákon setrvačnosti): Těleso setrvává v klidu nebo v rovnoměrném přímočarém pohybu, dokud není nuceno vnějšími silami svůj stav změnit.
- Newtonův druhý zákon: $\ve{a}=\ve{F}/m$, kde $F$ je síla, $m$ je hmotnost a $a$ je zrychlení.
- Newtonův třetí zákon: Působí-li těleso A silou na těleso B, pak těleso B musí působit silou stejné velikosti a opačného směru na těleso A.
- Třecí síla: $F_t = fF_n$, kde $F_n$ je normálová síla kolmá na podložku a $f$ je koeficient tření. Rozlišujeme statické tření (povrchy se vůči sobě nepohybují) a dynamické čili smykové tření. Třecí koeficienty se obvykle pohybují v rozsahu 0,1-0,8. Koeficient tření mezi suchou silnicí a pneumatikou je zhruba 0,6, koeficient tření ocel-ocel zhruba 0,2.
- Nakloněná rovina: Složka tíhové síly ve směru roviny je $F_1 = mg\sin\alpha$, kde $\alpha$ je úhel náklonu roviny. Složka tíhové síly kolmo na rovinu, neboli normálová síla, je $F_n = mg\cos\alpha$. Odtud plyne vztah pro velikost třecí síly na nakloněné rovině $F_t = fmg\cos\alpha$.
- Hybnost: $\ve{p} = m\ve{v}$, kde $m$ je hmotnost tělesa a $v$ jeho rychlost.
- Impuls síly: $\ve{F}\Delta t = \Delta\ve{p}$, kde $\Delta t$ je krátký časový interval působení síly a $\Delta p$ je změna hybnosti.
- Zákon zachování hybnosti izolované soustavy: $\sum \ve{p_i} = \text{konst}$. Izolovaná soustava těles znamená, že na tělesa nepůsobí žádná vnější síla s původem mimo tuto soustavu. Často také vyšetřujeme případ pohybu těles po rovině, kde na tělesa vertikálně působí gravitace, která je však kompenzována podpěrnou silou od podložky. V horizontálním směru vnější síly nepůsobí a hybnost v horizontální rovině se zachovává.
- Zákon zachování hybnosti při srážce dvou těles: $m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2$, $m_1$ a $m_2$ jsou hmotnosti těles a $u_1$, $u_2$, $v_1$ a $v_2$ jsou jejich počáteční a koncové rychlosti.