Baterie a elektrická energie
Za minutu proteče průřezem vodiče náboj o velikosti 3 C. Jaký protékal průměrný proud? Uveďte v jednotce mA.
Q = 3 C, t = 60 s, I = ?.
Vztah je I = Q/t = (3 C) / (60 s) = 1/20 A = 0,05 A = 50 mA.
Průměrný proud je 50 mA.
Jak velký náboj proteče průřezem vodiče, pokud po dobu jedné hodiny protéká proud o velikosti 2A? Uveďte v jednotce Coulomb.
t = 1 h = 3600 s, I = 2 A, Q = ?.
Vztah je Q = It = (2 A) · (3600 s) = 7200 C.
Proteče náboj o velikosti 7200 C.
Jednotka “A.h” bude nejspíše jednotkou
a) proudu; b) náboje; c) napětí; d) energie
Proud krát čas, tedy I · t, zřejmě vyjadřuje elektrický náboj.
Správně b) náboj.

Baterie mobilu má kapacitu 4385 mAh. Určete velikost náboje uschovaného v baterii mobilu, v jednotce Coulomb.
a) 3980 C; b) 15,8 kC; c) 862 C; d) 5,25 kC
Platí 1 A·h = (1 A) · (3600 s) = 3600 A·s = 3600 C.
Proto 1 mAh = 3,6 C.’
Odtud 4385 mAh = 4385 · 3,6 C = 15786 C ≈ 15,8 kC.
Správně b): 15,8 kC.
Mějme dvě baterie – první s kapacitou 2000 C a napětím 6 V, druhou s kapacitou 6000 C a napětím 1,5 V. Která z baterií obsahuje větší elektrickou energii?
a) obě stejně; b) druhá; c) první
E = QU. Pro první baterii je součin větší, tedy obsahuje více elektrické energie.
Správně c) první.
Baterie mobilu má kapacitu 3000 mAh. Po jak dlouhou dobu je schopna dodávat proud o velikosti 0,25 A?
Q = 3000 mAh = 3000 · 3,6 C = 10800 C.
I = 0,25 A; t = ?
t = Q/I = (10800 C) / (0,25 A) = 43200 s = 12 h.
Nebo jednodušeji bez přepočtu kapacity na Coulomby:
t = Q/I = (3 A·h) / (0,25 A) = (3/0,25) h = 12 h.
Baterie je schopna dodávat daný proud po dobu 12 h.
Určete elektrickou energii v Joulech, kterou je schopna dodat tužková baterie s kapacitou 1200 mAh, pokud předpokládáme konstantní napětí 1,5 V
Q = 1200 mAh = 1200 · 3,6 C = 4320 C.
U = 1,5 V; E = ?
E = QU = 6480 J = 6,48 kJ.
Energie baterie 6,48 kJ = 6480 J.
Mějme Li-ion baterii o kapacitě 2500 mAh. Pokud by se energie obsažená v baterii využila k ohřívání 1 litru vody, o kolik stupňů by ji ohřála?
a) o 19°C; b) o 8°C; c) o 34°C; d) o 3°C
Li-ion baterie dává napětí U ≈ 3,7 V. Shromážděný náboj Q = 2500 mAh = 9000 C. Energie v baterii je pak E = QU = 33300 J.
K ohřátí litru vody (1 kg) o jeden stupeň Celsia je potřeba asi 4200 J (vzpomeň na pojem měrná tepelná kapacita vody). Teplo 33300 J proto ohřeje litr vody o 33300 / 4200 ≈ 8°C.
Správně b) o 8°C.
Pokud z baterie odebíráme větší proud, tak napětí měřené mezi vývody baterie
a) zůstane stejné; b) stoupne; c) klesne
Při odběru většího proudu napětí mezi vývody baterie obecně o něco klesne (v důsledku úbytku napětí na vnitřním odporu baterie).
Správně c) klesne.
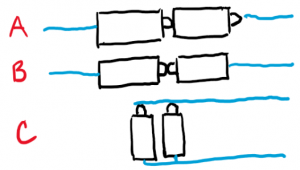
Máme dvě tužkové baterie 1,5 V. Pokud chceme získat zdroj o napětí 3 V, tak baterie zapojíme způsobem
a) A; b) B; c) C
Správně A. Sériové spojení opačnými póly k sobě vede k sečtení napětí.
Pro energii baterie používáme vztah E = QU. Pokud si ale vzpomenete, tak energie kondenzátoru byla E = QU/2. Vysvětlete, proč jsou vyjádření energie v těchto případech odlišná.
U baterie zůstává napětí mezi svorkami zhurba konstantní i v průběhu jejího vybíjení (napětí při vybíjení klesá jen mírně). Naproti tomu napětí mezi konci kondenzátoru je přímo úměrné náboji shromážděnému v kondenzátoru a tedy při vybíjení napětí kondenzátoru lineárně klesá. Průměrné napětí v průběhu vybití kondenzátoru je proto polovina maximálního počátečního napětí. Proto se jedna polovina vyskytuje i ve vztahu pro energii kondenzátoru.
Výkon elektrického proudu, kilowatthodina
Která veličina je vyjádřena takto: Spotřebovaná energie děleno doba?
a) práce; b) proud; c) výkon; d) příkon
Správně d) příkon.
Které z následujících vztahů dávají smysl?
a) P = Wt; b) P = W/t; c) W=t/P; d) W=Pt
Správně b) a d): P = W/t, W=Pt.
Jaký příkon má spotřebič, pokud za 2 hodiny spotřebuje energii 1 MJ?
a) 208 W; b) 104 W; c) 57 W; d) 139 W
E = 1 MJ; t = 2 h = 7200 s; P = ?
P = E/t = (1000000 J) / (7200 s) = 139 W.
Správně d): 139 W.

Jaký typický příkon má rychlovarná konvice?
a) 400 W; b) 20 kW; c) 50 W; d) 1500 W
Tepelné spotřebiče mají velký výkon (příkon), u konvice bývá okolo 1,5 kW = 1500 W.
Správně d) 1500 W.
Běžně jde sehnat akuvrtačku či jiné nástroje na baterii, avšak rychlovarná konvice na baterie se neprodává. Pokuste se vysvětlit proč.
Ohřívání vody spotřebuje mnoho energie a konvice musí mít oproti akuvrtačce větší příkon (výkon) a také musí na maximální výkon běžet delší dobu. Akumulátor pro rychlovarnou konvici by tak musel být velmi masivní a tedy i hodně drahý a jeho výdrž by byla spíš malá. Vrtačku je často potřeba používat v místech, kam je složité přivést napájecí kabel a kabel komplikuje práci. Vodu v konvici si naopak můžeme ohřát kdekoli. Pokud není k dispozici elektrický proud, tak je snadná možnost ohřívat na plynovém vařiči. Tedy akumulátor ke konvici by ani neposkytoval žádnou zásadní výhodu.
Jaký příkon má zařízení, pokud autoakumulátor o kapacitě 50 Ah a napětí 12 V vystačí po dobu 3 dny?
a) asi 8 W
b) asi 52 W
c) asi 22 W
d) asi 35 W
Q = 50 Ah; U = 12 V; t = 3 d = 72 h; P = ?
P = E/t = QU/t = (50 A·h) · (12 V) / (72 h) = (50 · 12 / 72) A·V = 8,3 W.
Správně a) asi 8 W.
Pokud je energie(práce) dodaná baterií dána vztahem W = QU, a zároveň víme, že příkon je dán jako P = W/t, pak lze odvodit, že příkon spotřebiče lze vyjádřit jako
a) P = Q/t; b) P = UI; c) P = U/I; d) P = QI
Do druhého vztahu dosadíme za W z prvního vztahu, tedy P = W/t = UQ/t. Dále víme, že I = Q/t. Proto platí P = UQ/t = UI.
Správně b) P = UI.

LED svítidlem připojeným do zásuvky na 230 V teče proud o velikosti 150 mA. Jaký je příkon svítídla?
Využijeme vztah získaný v minulé úloze: P = UI = (230 V) · (0,15 A) = 34,5 W.
Příkon svítidla je 34,5 W.
Jak velký proud teče rychlovarnou konvicí o příkonu 1,6 kW, která je v zásuvce? Zaokrouhlete na celé Ampéry.
Využijeme P = UI a vyjádříme I = P/U = (1600 W) / (230 V) ≈ 7 A.
Proud konvicí je asi 7 A.
Erik si doma zřídil kadeřnictví. Zásuvky má na 16 A jističi. Zajímalo by ho, kolik fénů o příkonu 800 W může provozovat zároveň, aniž by byl překročen nominální proud jističe.
a) 4; b) 6; c) 5; d) 3
Proud jedním fénem je I = P/U = (800 W) / (230 V) = 3,48 A. Nomilnální proud jističe vydělíme proudem potřebným pro jeden fén a dostaneme 16 A / 3,48 A = 4,6. Tedy postačí na provoz 4 fénů zároveň. Při zapojení pěti fénů už bude nominálí proud mírně překročen.
Správně a) 4 fény.
Helmut má doma zásuvkový okruh s 20 A jističem. Chce si pořídit několik PC na těžení bitcoinu, každý s příkonem 200 W. K tomu si chce ohřívat čínskou nudlovou polévku v mikrovlnce o příkonu 2,1 kW. Kolik PC si na těžbu může pořídit?
a) 12
b) 8
c) 19
d) 16
Proud jističe dovoluje příkon P = UI = (230 V) · (20 A) = 4600 W. Po odečtení mikrovlnky zbývá 2500 W. To stačí na 2500/200 = 12,5 PC.
Správně a) 12 PC.
Jak velkou energii spotřebuje motor s příkonem 1 kW za 1 hodinu? Uveďte v jednotce MJ.
Energie E = Pt = 1000 W · 3600 s = 3 600 000 W·s = 3,6 MJ.
Jakou veličinu měří jednotka kW.h? Dokážete napsat přepočetní vztah mezi jednotkou kWh a Joule?
Jedná se o součin výkonu a času, což je energie či práce. Přepočetní vztah jsme zjistili právě v předchozí úloze – 1 kWh je energie odpovídající příkonu 1 kW po dobu 1 h, přičemž E = Pt = 1000 W · 3600 s = 3 600 000 W·s = 3,6 MJ = 1 kWh.
Rychlovarná konvice má příkon 1,6 kW. Jak velkou energii spotřebuje za 5 minut? Uveďte v jednotce kWh i v jednotce Joule.
a) 0,133 kWh = 900 kJ
b) 0,133 kWh = 480 kJ
c) 0,250 kWh = 900 kJ
d) 0,250 kWh = 480 kJ
E = Pt = (1,6 kW) · (1/12 h) = 0,133 kWh
E = Pt = (1600 W) · (300 s) = 480 000 J = 480 kJ
Správně b) 0,133 kWh = 480 kJ

Lednice má průměrný příkon 120 W. a) Jak velkou energii spotřebuje za den? Určete v kWh. b) Kolik stojí roční provoz, pokud je cena 5 kč/kWh?
a) 6,52 kWh, 7453 kč
b) 2,88 kWh, 5256 kč
c) 1,44 kWh, 2628 kč
d) 4,28 kWh, 9482 kč
Energie E = Pt = (120 W) · (24·60·60 s) = 10 368 000 J
Energie E = Pt = (0,12 kW) · (24 h) = 2,88 kW·h za den.
Za rok to bude 2,88 kWh · 365 = 1051 kWh s cenou 1051 · 5 = 5256 kč.
Správně b) 2,88 kWh, 5256 kč.
Domácnost má běžně roční spotřebu 2 MWh elektrické energie. Jaký je průměrný příkon domácnosti? Kolik za rok zaplatí při ceně 5 kč/kWh?
a) 342 W, 15 tisíc kč
b) 228 W, 10 tisíc kč
c) 530 W, 15 tisíc kč
d) 126 W, 10 tisíc kč
Průměrný příkon P = E/t = (2000 kW·h) / (365 · 24 h) = 0,228 kW = 228 W.
Roční platba 2000 kWh · 5 kč/kWh = 10 tisíc kč.
Správně b) 228 W, 10 tisíc kč.
Jakou roční tržbu bude mít elektrárna Temelín, pokud 300 dnů v roce má elektrický výkon 2 GW a elektřinu bude prodávat při ceně 1,50 kč/kWh?
a) asi 13 mld kč
b) asi 37 mld kč
c) asi 6 mld kč
d) asi 22 mld kč
Nejprve spočteme vyprodukovanou elektrickou energii:
E = Pt = (2×106 kW) · (300 · 24 h) = 14400 ×106 kWh = 14,4 ×109 kWh.
Cena je (14,4 ×109 kWh) · (1,50 kč/kWh) = 21,6 ×109 kč.
Roční tržba bude asi 22 miliard korun.

*Li-ion baterie elektroauta Tesla S má hmotnost 544 kg a její energetická kapacita je 103 kWh. Naproti tomu z 1 kg benzínu spalovací motor získá mechanickou energii o velikosti asi 10 MJ. Porovnejte energetickou hustotu baterie a benzínu v nádrži. Co asi míníme energetickou hustotou (energy density)? Znáte přibližně výkon motoru vašeho auta? Jak dlouho by ho uvedená baterie uměla pohánět a kolik km by auto asi mezitím ujelo?
Energetická hustota, označme ɛ, vyjadřuje množství uschované energie na 1 kg materiálu (případně na 1 litr materiálu). Pro Li-ion baterii vychází ɛ = E / m = 103 kWh / 544 kg = 0,189 kWh/kg. Pro užitečnou energii benzínu vychází ɛ = 10 MJ / 1 kg = 10 MJ/kg = 2,78 kWh/kg. Energetická hustota benzínu je tedy asi 15-krát větší než pro baterii. Běžné osobní auto bude mít v nádrži asi 40 kg benzínu s dojezdem zhruba 500 km. Aby elektromobil měl stejný dojezd, tak baterie musí mít homtnost patnáctinásobnou, tedy asi 600 kg. Velikost a tíha baterií je velkou nevýhodou elektromobilů, protože auto musí tahat velkou zátěž navíc a samozřejmě tak velké akumulátory jsou také drahé.
Tepelný výkon a odpor
a) Vyslovte Ohmův zákon, b) zapište ho matematicky, c) vyjádřete z něj odpor
a) Velikost elektrického proudu kovovým vodičem je přímo úměrná velikosti napětí mezi jeho konci (a nepřímo úměrná odporu vodiče). b) I = U/R. c) R = U/I.
Bez počítání odhadněte, zdá má větší odpor žárovka s příkonem nominálním 40 W nebo 60 W.
a) obě stejný
b) 60 W
c) 40 W
Větší příkon bude odpovídat většímu proudu (obě žárovky jsou na stejném síťovém napětí). Aby proud byl větší, odpor vodiče musí být menší. Tedy žárovka s větším příkonem bude mít menší odpor a větší odpor bude mít žárovka s menším příkonem
Správně c) 40 W má větší odpor.
Nyní vypočítejte odpor žárovek 40 W a 60 W (tento příkon mají, pokud je připojíme na 230 V). Využijte i Ohmův zákon.
a) 1322 Ω a 621 Ω
b) 674 Ω a 882 Ω
c) 882 Ω a 588 Ω
d) 1322 Ω a 882 Ω
Z Ohmova zákona víme, že R = U/I. Proud neznáme, umíme ho však určit na základě příkonu P a napětí U, jelikož P = UI, tedy I = P/U.
Pro 40 W žárovku máme: I = P/U = (40 W) / (230 V) = 0,174 A. Odpor je potom R = U/I = (230 V) / (0,174 A) = 1322 Ω.
Pro 60 W žárovku máme: I = P/U = (60 W) / (230 V) = 0,261 A. Odpor je potom R = U/I = (230 V) / (0,261 A) = 882 Ω.
Správně d) 1322 Ω a 882 Ω.
Napište obecný vztah mezi příkonem spotřebiče, jeho odporem a napětím, na které je připojený. Vyberte všechny správné vztahy.
V předchozí úloze jsme počítali odpor ze vztahu R = U / I, přičemž za proud jsme dosazovali I = P/U. Dohromady tak máme R = U/I = U/(P/U) = U2/P.
Nebo také naopak P = U2/R.
Jaký odpor má topná spirála konvice s nominálním příkonem 1,5 kW?
a) 48 Ω
b) 21 Ω
c) 64 Ω
d) 35 Ω
Vzpomeneme si, že konvice je v zásuvce na napětí 230 V. Zde již můžeme využít dříve odvozený vztah R = U2/P = 2302 / 1500 = 35,3 Ω.
Odpor spirály konvice je asi 35 Ω.
Topnou spirálou o odporu 15 Ω prochází proud o velikosti 10 A. Jaký je příkon této spirály? (Spirála není připojena na 230 V)
Známe odpor R a proud I, chceme určit příkon P. Víme, že P = UI. Musíme však určit U. Víme ale z Ohmova zákona, že
U = RI = 15 · 10 = 150 V.
Příkon potom je P = UI = (150 V) · (10 A) = 1500 W.
Nyní již jen dosadíme P = RI2 = 15 · 102 = 1500 W.
Příkon spirály je 1500 W.
Napište obecný vztah mezi příkonem spotřebiče, jeho odporem a proudem, který jím prochází.
Známe odpor R a proud I, chceme určit příkon P. Víme, že P = UI. Musíme však určit U. Víme ale z Ohmova zákona, že U = RI. Tento vztah dosadíme do předchozího:
P = UI = RI · I = RI2.
Co bude více topit – a) vodič o odporu 10 Ω mezi jehož konci je napětí 12 V, nebo b) vodič o odporu 5 Ω, jímž protéká proud o velikosti 1,5 A?
a) vodič s odporem 10 Ω a napětím 12 V
b) vodič s odporem 5 Ω a proudem 1,5 A
c) budou topit stejně
Tepelná výkon prvního vodiče je P1 = U2/R = 14,4 W, tepelný výkon druhého vodiče je P2 = RI2 = 11,25 W. Tepelný výkonn prvního vodiče je tedy větší.
Správně a) vodič s odporem 10 Ω a napětím 12 V má větší výkon.
Mějme zdroj konstantního napětí. Nejprve k němu připojíme rezistor o odporu 10 Ω a potom rezistor o odporu 50 Ω. Který bude víc topit?
a) oba stejně
b) 10 Ω
c) 50 Ω
Využijeme vztah P = U2/R. Připojujeme na stejné napětí, tedy je patrné, že rezistor s menším odporem má větší výkon a tedy více topí. Je to jasné i z úvahy, že na rezistorech je stejné napětí a větší proud protéká menším rezistorem.
Správně b) 10 Ω více topí.
Ke zdroji napětí připojíme sériově za sebe odpory 50 Ω a 200 Ω. Který bude více topit?
a) 50 Ω
b) oba stejně
c) 200 Ω
Při sériovém spojení je proud oběma rezistory stejný a úbytek napětí na rezistoru s vyšším odporem je větší. Podle vztahu P = UI tedy usoudíme, že vyšší odpor znamená vyšší napětí a tedy větší výkon.
Správně c) 200 Ω bude více topit.
Ke zdroji napětí připojíme paralelně k sobě odpory 50 Ω a 200 Ω. Který bude více topit?
a) 200 Ω
b) 50 Ω
c) oba stejně
Při paralelním spojení je napětí na obou rezistorech stejné a proud je větší v rezistoru s nižším odporem. Více tedy topí rezistor s nižším odporem.
Správně b) 50 Ω bude více topit.
Pepíček má nekvalitní prodlužovačku s odporem 3 Ω. Tu zapojí do zásuvky na 230 V a připojí do sekačky. Prodlužovačkou pak teče proud o velikosti 6 A. Kolik procent celkové elektrické energie se ztratí ve formě tepla na prodlužovačce?
a) 14%
b) 5%
c) 2%
d) 8%
Tepelná ztráta na prodlužovačce je P = RI2 = 3 · 62 = 108 W.
Celkový výkon na spotřebiči a prodlužce je P = UI = 230 · 6 = 1380 W.
Na tepelné ztráty na prodlužce tak padne 108/1380 = 0,078 = 7,8 %.
Správně d) asi 8%.
Jak se změní ztrátový výkon na dálkovém vedení, pokud přenosové napětí zvedneme na trojnásobek?
a) 3x vzroste
b) 6x vzroste
c) 9x vzroste
d) 3x klesne
e) 9x klesne
Ztrátový výkon na vedení lze určit jako P = RI2. Přenosové vedení má za úkol přenášet výkon P = UI. Pro přenesení stejného výkonu při trojnásobním napětí stačí třetinový proud. Ztrátový výkon je úměrný druhé mocnině proudu a tedy bude 1/32 = 1/9 původní hodnoty. (Pozor, argumentaci nemůžeme založit na vztahu P = U2/R, protože zde U je napětí mezi konci vodiče / vedení, což je něco úplně jiného než přenosové napětí, které bývá např. 110 kV.)
Správně e) ztráty 9x klesnou.
*Pepíček má zdroj napětí 230 V (zásuvka) a dvě topné spirály, které mají při připojení na 230 V příkon 500 W a 1000 W. Přemýšlí, zda je má zapojit sériově nebo paralelně. Nejprve odhadněte, ve kterém případě si vice zatopí. Potom vypočítejte tepelné výkony spirál v obou případech.
a) paralelně 1500 W, sériově 666 W
b) sériově 1500 W, paralelně 333 W
c) paralelně 1500 W, sériově 333 W
d) sériově 1500 W, paralelně 666 W
Větší výkon bude jistě při paralelním spojení, protože obě spirály budou na stejném maximálním napětí 230 V. Odpor paralelního spojení je menší a tedy celkový proud bude větší než v případě sériového spojení. Při paralelním spojení je celkový výkon součtem samostatných výkonů, tedy 1500 W. Ze zadání je zřejmé, že 500 W spirála má dvojnásobný odpor než 1000 W spirála. Při sériovém spojení tak máme vlastně spirálu s odporem troojnásobným oproti samostatné 1000 W spirále. Výkon pak bude třetinový, neboli 333 W (Vycházíme ze vztahu P = U2/R).
Správně c) paralelně 1500 W, sériově 333 W.
Elektrickým vedením se přenáší elektrická energie, potažmo elektrický výkon – např. je potřeba přenášet výkon 10 MW. Při přenosu na dlouhé vzdálenosti se transformuje na vysoké napětí. Prý se zmenší ztráty. Dokážete vysvětlit proč?
Přenosové vedení má za úkol přenášet výkon P = UI. Pro přenesení stejného výkonu při vyšším napětí stačí menší proud. Ztrátový výkon je určen vztahem P = RI2, kde R je odpor vedení. Menší proud tedy znamená menší ztrávový výkon, a to dokonce s druhou mocninou.