úloha 1
Hotel na ostrově v Karibiku inzeruje: „U nás každý rok svítí slunce 350 dní!“ Je-li reklama pravdivá, určete nejmenší počet dní, které si musí váš/vaše třídní v hotelu v roce 2025 rezervovat, aby měl absolutní jistotu, že bude mít určitě dva po sobě jdoucí slunečné dny.
řešení: Zamračených dnů je 365 – 350 = 15. Nejméně příznivá situace nastane, když návštěvník přijede za slunečného dne a pak se začnou střídat vždy jeden zamračený a jeden slunečný den. Takto proběhne 31 dnů a ještě bude potřeba počkat na další den, aby konečně byly dva po sobě slunečné. Celkem tedy je potřeba objednat aspoň 32 dnů. Popsaný průběh je možno znázornit takto (O=slunce, X=mraky):
O X O X O X O X O X O X O X O X O X O X O X O X O X O X O X O O
úloha 2
Eliška našla velkou houbu, která měla hmotnost 1 kilogram a 99 % její hmotnosti byla voda. Jaké množství vody by se z houby muselo odpařit, aby houba obsahovala už jen 98 % vody?
řešení: Na začátku je v houbě 990 g vody a 10 g sušiny. Voda se pak odpařuje a sušina zůstává. Sušiny i na konci bude 10 g, což má ve finále tvořit 2% hmotnosti. Celková hmotnost tak je padesátinásobek, čili 500 g, z toho 490 g vody. Muselo se tedy odpařit právě 500 g vody, čili půl kila.
úloha 3
Na provázek zavěsíme kuličku, čímž dostaneme kyvadlo jako na obrázku. Potom kuličku necháme zhoupnout, přičemž provázek se zarazí o nějakou tyčku (na obrázku hřebík). Jak se bude dál pohybovat kulička? Bude se pohybovat po kružnici? Omotá se provázek kolem hřebíku? Pokud ano, omotá se jednou nebo vícekrát? Vyzkoušejte a popište výsledek.
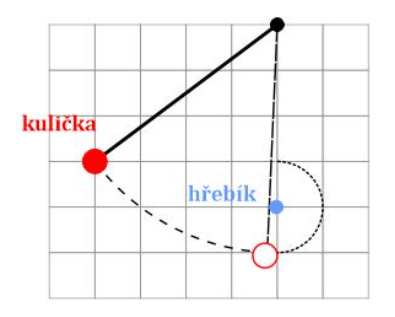
řešení: V obrázku si můžeme všimnout, že aby se kulička aspoň jednou omotala, musela by vystoupat přesně do výšky, ve které svůj pohyb začala. Pokud bychom na začátku kuličku jen volně pustili a nepostrčili ji, tak by určitě nemohla vystoupat výš, než kde začala. V důsledku ztráty energie třením a odporem by kulička byla spíš schopna vystoupat jen o trochu níž, než kde začala. Když jste prováděli experiment, tak bylo těžké nastavit situaci přesně jako na obrázku, takže vám to mohlo vyjít různě. Pokud jste kuličce na počátku udělili postrčením nějakou rychlost, tak se mohla začít obtáčet kolem hřebíku. Plný počet bodů jsem uděloval za jakýkoli rozumný podrobnější popis, jak probíhal váš experiment. Čtenáři od tercie výš již znají pojem potenciální a kinetická energie. Mohli bychom říci, že kulička na počátku má jen potenciální energii. Ta se při klesání kuličky přeměňuje na kinetickou a při stoupání kuličky zpět na potenciální. V důsledku zákona zachování energie tak kulička nemůže vystoupat výš než začala, pokud ji neudělíme počáteční postrčení, čili počáteční kinetickou energii. Pozorný čtenář si možná všimne ještě jednoho detailu: Kromě kuličky se pohybuje a mění polohu i provázek. Při namotávání na hřebík bude těžiště provázku určitě níže, než bylo na počátku, což by mohlo usnadnit namotání na hřebík (v případě, že provázek nemá zanedbatelnou hmotnost). Podrobnější úvahy však nechám na vás…
(úloha byla převzata z Neadventního kalendáře fyziky https://kdf.mff.cuni.cz/neadventni-kalendar/)
úloha 4
Pepa si myslí dvě čísla. V obou číslech není žádná jiná číslice než 1 a součet těchto dvou čísel se rovná součinu těchto dvou čísel. Jaká dvě čísla si Pepa myslí?
řešení: Jedná se o čísla 11 a 1,1. Součet i součin jsou 12,1.
úloha 5
Michal měl k dispozici 125 malých kostek. Z některých z nich slepil velkou kostku s devíti tunely procházejícími celou kostkou tak, jak je znázorněno na obrázku. Kolik malých kostek přitom nepoužil?
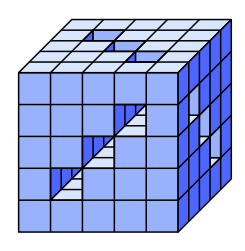
řešení: Devět tunelů o délce pět kostek odpovídá počtu 45 vynechaných kostek. Tunely se ale protínají, takže jsme některé započítali vícekrát a vynechaných kostek bude méně než 45. Pozorným pohledem si všimneme, že není žádné místo, kde by se protínaly jen dva tunely. Naopak existují tři místa, kde se protínají vzájemně tři tunely. Tedy do počtu 45 jsme tři kostičky započítali každou třikrát, ale měli jsme je započítat jen jednou. Započítali jsme tedy 6 kostiček navíc a celkový počet vynechaných kostiček je
45 – 6 = 39.
Zdroje úloh
Matematický klokan, Neadventní kalendář fyziky, vlastní archiv.