Jedná se o postřehy z první vyučovací hodiny na téma zrychlený pohyb, první ročník SŠ (čtyřleté G).
- Téma jsme začali diskusí volného pádu – pustil jsem míček a ptal se, zda se pohybuje stále stejnou rychlostí či ne – hlasování.
- Míček pustím nad hlavou z výšky ca. 2 m. Otázka – padá déle než 1 s nebo kratší dobu?
- Jakou rychlostí poletí, kdyby letěl právě 1 s, 2s, 3s? Tipujeme. Při té příležitosti si několik studentů vzpomnělo na hodnotu gravitačního zrychlení. Každou sekundu míček zrychlí o 10 m/s – čili zrychlí o 10 m/s za sekundu. Nakreslíme obrázek jako dole. Zapíšu $g \approx 10$. Otázka – jakou má g jednotku? Opakuji a píšu předchozí větu, ze které plyne jednotka m/s2.
- Jakou vzdálenost míček uletí za 1 s, tedy o kolik se propadne za 1 s? Tipujeme. Pokud někdo tipuje méně než 2 m, znovu zopakuji puštění míčku z výšky 2 m – padá kratší dobu než 1 s. Odpověď je 5 metrů. Začneme kreslit tabulku jako dole.
- Jakou vzdálenost míček uletí za 2 s? Tipujeme. A za 3 s? Tipujeme. Když se někdo trefí doplníme do tabulky.
- Ve chvíli, kdy v tabulce máme uražené dráhy za 1 s, 2 s, 3 s, ptám se na dráhu za 4 s. Pobídnu studenty, že v tabulce možná začnou vidět nějaké pravidlo? Pokud pravidlo nevidí, jistě někdo ještě správně tipne dráhu za 4 s. Možná pravidlo začnou vidět teď.
- Dříve či později někdo uvidí pravidlo: čas násobím rychlostí a vydělím dvěma, tedy $s = vt/2$.
- Vztah připomíná $s = vt$ pro rovnoměrný pohyb. Proč se tam ale dělí dvěma? Je užitečné si vztah napsat ve formě $s = \frac{v}{2}t$. Možná někdo přijde na to, že $v/2$ je údaj o průměrné rychlosti.
- Šlo by vysledovat i jiné pravidlo? V jednotce gravitačního zrychlení je sekunda na druhou. Šlo by najít pravidlo, kde bude vystupovat druhá mocnina času? Možná někdo přijde na to, že pravidlo by mohlo být $s = 5t^2$, nebo si všimnout, že když se čas zvětší dvojnásobně, tak dráha naroste čtyřnásobně, když čas vzroste 3x, tak dráha naroste 9x atd.
- Takto k zákonitostem volného pádu. Osvědčilo se tipování uražené dráhy. Vtáhne to i studenty, kteří jsou jinak ztraceni a mohou se trefit a odpovědět správně.

- Zrychlení může být i jiné než při volném pádu, např. zrychlení auta. Teď zavedeme obecně veličinu zrychlení: přírůstek rychlosti za 1 sekundu, nebo $a = \Delta v / \Delta t$, tedy změna velikosti rychlosti za nejaký časový úsek.
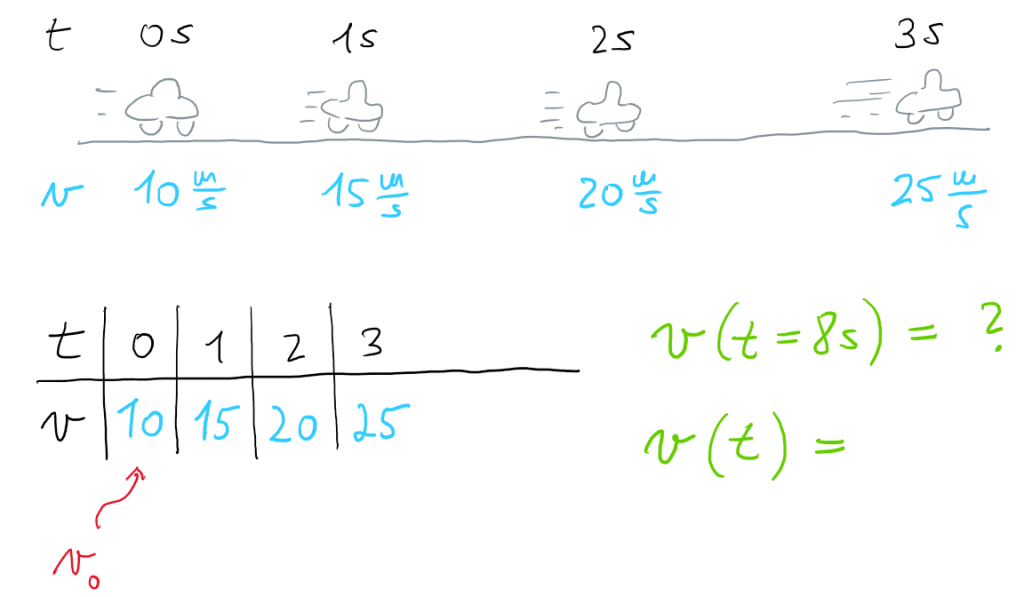
- Nyní máme případ zrychlujícího polozávodního auta, které vyjíždí z benzínky na dálnici. Nejdřív jede rychlostí 10 m/s a poté zrychluje. Nakreslím obrázek jako níže a k tomu tabulku.
- Otázky – Jaká je velikost zrychlení auta? Jakou rychlost bude mít auto v čase t = 8 s? Půjde nějak napsat předpis pro rychlost auta v libovolném čase t, pokud předpokládáme kouzelné auto, které může zrychlovat do nekonečna? Dojdeme tak postupně ke vztahu $v = v_0 + at$.
- Bylo pro mě překvapivé, kolik studentů nebylo schopno určit dráhu v čase t = 8 s, přestože by stačilo jen doplnit tabulku až do čísla 8 a rychlost vždy zvětšit o 5, tedy doplnit jednoduchou číselnou řadu. Studenti byli zjevně ve “školním módu”, kdy vypnuli selský rozum a byli připraveni používat jen nějaké školské přesně dané postupy, které však v tomto případě ještě nebyly zavedeny. Přitom doma na gauči by na správně řešení jistě přišli během pár sekund. Následovala poučná litanie o tom, že mají i ve škole používat selský rozum a snažit se problém vyřešit jakkoli a ne jen nějakým předem daným naučeným postupem.