- Termika, vnitřní energie, teplota, teplo
- Přenos tepla
- Látkové množství a molární veličiny
- Plyny – stavová rovnice, izoděje, adiabatický děj
- Práce plynu, tepelné stroje
- Pevné látky – struktura, pevnost, pružnost
- Kapaliny – povrchové napětí, kapilární jevy, teplotní roztažnost
- Změny skupenství – tání, tuhnutí, sublimace
- Změny skupenství – vypařování, var, sytá pára, kondenzace
Termika, vnitřní energie, teplota, teplo

1. Vysvětlete jevy Brownův pohyb a difuze – proč k nim dochází? Uveďte příklady, kdy dochází k difuzi.
Brownův pohyb (1827) – chaotický pohyb pylového zrnka ve vodě pod mikroskopem v důsledku náhodných nárazů okolních částic vody. Difuze – šíření látky do celého dostupného objemu (kapalina, plyn) v důsledku chaotického pohybu molekul. Úhrnně se jeví jako pohyb částic z místa o vyšší koncentraci do místa o nižší koncentraci.
2. Jak spolu souvisí teplota a rychlost neuspořádaného pohybu částic, potažmo kinetická energie částic?
Vyšší teplota → vyšší střední kinetická energie částic, tedy i jejich rychlost. Teplota je přímo úměrná střední kinetické energie a přímo úměrná střední kvadratické rychlosti (druhá mocnina rychlosti).
3. Popište aspoň tři různé způsoby (fyzikální principy), na jejichž základě se měří teplota.
Teplotní roztažnost kapaliny (lihový, rtuťový teploměr), teplotní roztažnost kovů (bimetalový pásek); změna elektrického odporu – zejména polovodiče (termistor) vykazují výrazný pokles odporu při rostoucí teplotě; intenzita a vlnová délka infračerveného záření (termokamery či určování teploty hvězd); termoelektrický jev (termočlánek pro měření velmi vysokých teplot) a další.
4. Jako teploměrné kapalina se často používá líh. Proč se používá líh, a nikoli obyčejná voda? V jakém rozsahu teplot jde lihovým teploměrem měřit?
Rozsah je omezen teplotou tuhnutí a teplotou varu. Vodním teploměrem by nešlo měřit pod bodem mrazu, zatímco teplota tuhnutí etanolu je -114°C. Lihovým teploměrem naopak není možné měřit vyšší teploty než ~70°C, protože jeho teplota varu je 78°C. Líh má také výrazně vyšší koeficient teplotní roztažnosti než voda. V neposlední řadě objem vody neroste lineárně s teplotou (tzv. anomálie vody), tedy voda není vhodná.
5. Popište Celsiovu a Kelvinovu teplotní stupnici. Převeďte 37°C, 111 K. Vysvětlete pojem absolutní nula.
Stupnice Celsia dělí interval mezi teplotou tání a teplotou varu vody na 100 dílů. Stupnice Kelvina zavádí stupeň o stejné velikosti, akorát nula stupňů není přisouzeno teplotě tání vody, nýbrž stupnice začíná na absolutní nule. To je nejnižší myslitelná teplota, kdy ustane tepelný pohyb částic (či přesněji kdy je neuspořádaný pohyb nejmenší možný), odpovídá tomu teplota -273,15 °C.
- Tedy 37°C = 310, 15 K a 111 K = -162,15 °C.
6. V USA se používá teplotní stupnice Fahrenheita. Referenčnní body stupnice: 0°F … teplota tuhnutí jakési směsi soli s vodou; 96°F … teplota lidského těla. Platí dále 32°F … bod tání ledu; 212°F … bod varu vody.
a) Sestrojte převodní vztahy: [°F] = a[°C] + b; [°C] = c[°F] + d
b) Kolik stupňů Celsia je při teplotě vzduchu 60°F? Kolik stupňů Fahrenheita je při teplotě -15°C?
c) Je nějaká teplota, při které jsou údaje °C a °F stejné?
a/ Ze zadání máme 32[F] = a ⋅ 0[C] + b; 212[F] = a ⋅ 100[C] + b. Z první rovnice ihned plyne b = 32. Dosazením b do druhé pak a = 1,8. Ve výsledku [°F] = 1,8[°C] + 32. Vyjádřením [°C] z rovnice máme [°C] = ([°F] – 32) / 1,8.
b/ Proto 60°F = (60 – 32) / 1,8 = 15,6°C; a také -15°C = (-1,8
c/ Pro jakou teplotu jsou údaje [°F] a [°C] stejné? Označme neznámou teplotu T. Využijeme třeba první převodní vztah a máme T = 1,8T + 32 a tedy -0,8T = 32, tudíž T = -40°C = -40°F.
- a) [°F] = 1,8[°C] + 32. b) [°C] = ([°F] – 32) / 1,8. c) -40°C
7. Z jakých dvou základních složek se skládá vnitřní energie látky? Dejte příklady nějakých dějů, při kterých se mění jedna složka a při kterých se mění druhá složka.
Kinetická a potenciální složka. Při zahřívání plynu se mění hlavně kinetická složka (neuspořádaný pohyb). Potenciální složka vyplývá ze vzájemné polohy molekul, jejich vzdáleností, jejich uspořádání. Potencální složka se mění třeba při chemických reakcích nebo změnách skupenství. Např. při vypařování se mění kinetická složka na potenciální složku. Potenciální složka se výrazně mění i při chemických reakcích.
8. Co má vyšší vnitřní energii – kapalná voda, nebo vodní pára o stejné teplotě? Proč?
Vodní pára má vyšší vnitřní energii. Voda i pára mají stejnou teplotu, tedy shodnou kinetickou složku vnitřní energie. Pára má ovšem vyšší potenciální energii, protože pro odpaření musela být vykonána práce na vyvázání molekul z vazeb v kapalině – neboli muselo být dodáno skupenské teplo vypařování.
9. Vyslovte první termodynamický zákon – jednak matematickou formulaci a jednak slovní formulaci
ΔU = Q + W. Jedná se v podstatě o zákon zachování energie. Změna vnitřní energie je rovna součtu tepla dodaného systému a práci vykonané na systému. V případě, že systém koná práci, tak W má ve vztahu záporné znaménko.
10. Plyn ve válci s pístem přijal teplo o velikosti 700 J a rozpenul se, přičemž vykonal práci 500 J. Jak se změnila vnitřní energie plynu? Má plyn výsledně vyšší nebo nižší teplotu než na počátku?
ΔU = Q + W = 700 J – 500 J = 200 J. Vnitřní energie plynu naroste o 200 J, teplota plynu se zvýší.
- U naroste o 200 J.
11. Helmut si nechce spálit jazyk, a proto smíchal 350 ml čaje o teplotě 90°C se 150 ml vody o teplotě 20°C. Jaká je výsledná teplota nápoje?
Mícháme kapaliny stejného druhu a proto stačí použít vážený průměr: (90
Výsledná teplota 69°C.
12. Štěpán má na stole plastovou láhev s teplým pivem o teplotě 25°C a zároveň studenou vodu o teplotě 4°C. Chce si namíchat půllitr ředěného piva o příjemné teplotě 10°C. Kolik použije teplého piva a kolik studené vody?
Pivo je téměř voda a tedy mícháme kapaliny (téměř) stejného druhu. Množství piva označme x, množství vody y. Platí y = 0,5 – x. Použijeme vztah pro vážený průměr:
(25° ⋅ x + 4°C ⋅ y)/(x+y) = 10°C.
Tedy (25x + 4[0,5 – x])/0,5 = 10.
Upravíme na 21x + 2 = 5, a tedy x = 1/7 litru, y = 5/14 litru.
- Teplého piva 1/7 ≈ 0,14 litru, studené vody 5/14 ≈ 0,36 litru.
13. Váleček z neznámého kovu o teplotě 90°C a hmotnosti 200 g byl ponořen do tepelně izolované nádoby s vodou o hmotnosti 0,6 kg a teplotě 15°C. Teplota vody a válečku se ustálila na 20°C. Jaká je měrná tepelná kapacita materiálu? O jaký by se mohlo jednat materiál?
Teplo odezdané válečkem je rovno teplu přijatému vodou. Tepelná kapacita vody je c = 4200 J/kg/K. Neznámou kapacitu označme x. Potom
900 J/kg/K. To by snad mohl být hliník.
14. Do vody o objemu 2 litry a teplotě 20°C byl vložen železný předmět o hmotnosti 0,5 kg. Výsledná teplota po dosažení rovnovážného stavu je 28°C. Celý děj se odehrává ve velmi dobře tepelně izolované termosce. Jakou teplotu měl železný předmět před vložením do vody, jestliže tepelná výměna nastala jen mezi železem a vodou?
Vyjdeme z toho, že teplo odevzdané železem musí být rovno teplu, které přijme voda, přičemž se nakonec obojí ustálí na teplotě
Počáteční teplota železa 327°C.
Přenos tepla
15. Popište tři hlavní mechanismy přenosu tepla.
Vedení – předávání energie kmitání sousedním molekulám; proudění – zahřátá tekutina teplotní roztažností zvětší objem a zmenší hustotu, podle Archimedova zákona stoupá a tím přenáší teplo vzhůru, tekutina se tím promíchává; zářením – všechny objekty o nenulové termodynamické teplotě vydávají elektromagnetické záření, obvykle zejména infračervené. Čím teplejší objekt, tím kratší vlnová délka záření.
16. Vysvětlete, které materiály jsou dobré tepelné vodiče a které naopak dobré tepelné izolanty. Jaké společné vlastnosti mají materiály v rámci těchto skupin?
Velmi dobré tepelné vodiče jsou kovy (souvisí i s elektrickou vodivostí). Dobré izolanty jsou plyny. Proto i materiály s velkým objemovým obsahem plynu jsou dobré izolanty – polystyren, minerální vata, molitan atp. Tyto materiály obsahují bublinky plynu, či jsou porézní s mnoha malými kapsičkami plynu. Rozdělením do malých kapsiček se navíc velmi omezí přenos tepla prouděním plynu.
17. Jaké jsou strategie omezování tepelných ztrát budov?
Izolace stěn polystyrenem nebo minerální vatou, důležitá je zejména izolace střechy (stropu) minerální vatou či foukanou izolací. Významné tepelné ztráty okny – trojitá skla, mezi skly plyn, rozdělení do více komor omezuje přenos tepla prouděním.
18. Popište princip termosky.
Mezi oddělenými stěnami plyn, a to nejlépe plyn o významně sníženém tlaku. Je tak možný jen přenos tepla zářením. Lesklá kovová stěna navíc odráží záření.
19. Šimon si chce v garáži zřídit vlastní bydlení a kancelář. Garáž má rozměry 4x3x5m. V garáži chce udržovat stálou teplotu 20°C, přičemž průměrná roční teplota je 8°C. Stěna garáže je z cihel a má tloušťku 20 cm. Jaké budou roční náklady na topení, pokud je vytápěno elektricky při ceně 6 kč/kWh? Předpokládejte stejný přestup tepla i do podlahy a stropu. Součinitel tepelné vodivosti cihel je 0,8 W/m/K.
Pro tepelné ztráty máme vztah
Q = t ⋅ S ⋅ λ ⋅ ΔT / d.
Rok je t = 365 ⋅ 24 ⋅ 3600 s = 31,536 × 106 s; plocha stěn garáže celkem S = 2 ⋅ (12 + 15 + 20) = 94 m2; λ = 0,8 W/m/K; rozdíl teplot 12°C, tloušťka stěny d = 0,2 m. Vše máme v základních jednotkách a dosadíme: Q = 35,6 GJ = 9881 kWh = 9,88 MWh. Náklady pak necelých 60000 kč. Hodně, že? Výsledek je jen velice přibližný. Navíc mnoho dní v roce je teplota >20°C, což zvyšuje údaj o průměrné teplotě.
- Náklady necelých 60000 kč/rok.
20. Na kolik procent původní hodnoty se sníží náklady na vytápění, když se cihlová stěna tloušťky 20 cm (λ = 0,8 W/m/K) zateplí polystyrenem tloušťky 10 cm o tepelné vodivosti 0,03 W/m/K?
Zde je vhodné definovat tepelný odpor R = d/λ. Čím větší tepelný odpor, tím menší ztráty. Spojení cihel a polystyrenu se chová jako sériové spojení tepelných odporů, tedy R = R1 + R2.
Zde R1 = (0,2 m) / (0,8 W⋅m-1⋅K-1) = 0,25 m2⋅K⋅W-1;
R2 = (0,1 m) / (0,03 m2⋅K⋅W-1) = 3,33 m2 K W-1.
Tedy odpor se změní z původních 0,25 na (3,33 + 0,25) = 3,58 m2 K W-1 . To je nárůst odporu 14,3 × a stejným faktorem poklesnou ztráty – to je pokles na 7 % původní hodnoty, tedy zlepšení o 93 %. Tepelné ztráty se zmenší o 93%, tedy na 7%.
Látkové množství a molární veličiny
21. Vodík je v periodické tabulce první prvek, helium druhý, uhlík šestý, dusík sedmý a kyslík osmý. Na základě uvedeného odhadněte molární hmotnosti H2, He, C, N2, O2, CO2. Uran je v tabulce na 92. místě. Můžeme použít stejný systém odhadu molární hmotnosti? Proč?
Nejběžnější izotopy lehkých prvků mají stejný počet protonů jako neutronů. Molární hmotnost prvku přibližně odpovídá počtu nukleonů. Proto přibližně H2: 2 g/mol; He 4 g/mol; C: 12 g/mol; N2: 28 g/mol; O2: 32 g/mol; CO2: 44 g/mol. Uran má 92 protonů, ale výrazně víc neutronů. Nejběžnější izotop má 238 nukleonů.
22. Mějme železnou kostku o straně 10 cm.
a) Kolik atomů železa je v této kostce? Potřebné hodnoty vyhledejte.
b) Určete na základě toho, jaké jsou přibližné vzdálenosti mezi jednotlivými atomy železa, pokud pro jednoduchost předpokádáme, že atomy leží v uzlových bodech krychlové sítě (kubická krystalová soustava)
Molární hmotnost železa M
Látkové množství
Počet atomů
Jedna krychlová buňka má osm vrcholů a v každém atom, avšak o atom se dělí osm buněk, tedy na každou buňku v každém vrcholu připadne osmina atomu a tedy jeden celý atom na jednu buňku. Počet atomů odpovídá počtu buněk. Proto velikost strany buňky
a) 8,5×1025 částic, b) 0,23 nm
23. a) Určete hmotnost, objem a látkové množství oxidu uhličitého, který vznikne úplným spálením 4 kg metanu. b) Kolik kilogramů vzdušného kyslíku se při této reakci spotřebuje?
a) Reakce po vyčíslení: CH4 + 2O2 → CO2 + 2H2O.
Molární hmotnost metan Mm(met) = 16 g/mol; Mm(CO2) = 44 g/mol; Mm(O2) = 32 g/mol.
Látkové množství metanu nmet = 4000 g / (16 g mol-1) = 250 mol.
Na jednu molekulu metanu vznikne shořením 1 molekula CO2. Proto vznikne i 250 mol CO2.
m(CO2) = n⋅ Mm = (250 mol) ⋅ (44 g/mol) = 11000 g = 11 kg.
Za normálních podmínek (0°C, 101 kPa) by to byl objem
V = n ⋅ 22,4 L/mol = 5600 litrů = 5,6 m3 CO2.
b) Spotřebované látkové množství O2 je dvojnásobné, tedy 500 mol, hmotnost je
(500 mol) ⋅ (32 g/mol) = 16000 g = 16 kg spotřebovaného kyslíku.
a) CO2: 250 mol, 11 kg, 5600 litrů za norm. podmínek. b) 16 kg kyslíku.
Plyny – stavová rovnice, izoděje, adiabatický děj

24. Rozhodněte, která tvrzení jsou pravdivá a která nepravdivá. Ta nepravdivá opravte.
a) Teplota plynu je přímo úměrná průměrné rychlosti částice plynu.
b) Při dané teplotě se všechny částice pohybují stejně rychle.
c) Při stejné teplotě se molekuly dusíku ve vzduchu pohybují rychleji než molekuly CO2.
d) Ideální plyn je nestlačitelný.
e) Kalorie je jednotkou energie.
f) Při izochorickém ději je tlak přímo úměrný teplotě.
g) Při adiabatickém ději plyn nekoná práci.
h) Při izotermickém ději je tlak přímo úměrný objemu.
i) Při izobarickém rozpínání plynu se jeho teplota zvyšuje.
j) Při izotermickém ději se nemění vnitřní energie plynu.
k) Při uzavření jednoho cyklu termodynamického tepelného stroje je celková vykonaná práce nulová.
l) Při adiabatické kompresi se teplota plynu zvyšuje.
Správně: c, e, f, i, j, l. Ostatní nesprávně.
25. Změní-li se teplota ideálního plynu za neměnného objemu z 20 °C na 40 °C, zvýší se tlak dvakrát, méně než dvakrát, nebo více než dvakrát?
Méně než dvakrát – ve všech výpočtech musíme uvažovat termodynamickou teplotu v Kelvinech.
26. Helmut zavařuje třešňový kompot. Napadla ho otázka: Pokud zavře zavařovací sklenici, ve které je jen vzduch, a ohřeje ji ve vroucí vodě, jaký bude výsledný tlak ve sklenici? Kolikrát stoupne? Co kdyby na začátku bylo ve sklenici trochu vody? Bude nárůst tlaku stejný?
Izochorický děj, ohřátí z 293 K na 373 K. Tedy nárůst teploty 373/293-krát ≈ 1,27×. Počáteční tlak 100 kPa, koncový tedy asi 127 kPa. Pokud na začátku bude trochu vody, tak se dost vody může odpařit, čímž více vzroste tlak (více částic v plynném stavu).
Tlak stoupne 1,27-krát, tedy ze 100 kPa na 127 kPa.
27. Yennefer si hraje s injekční stříkačkou. Uzavřela do ni 8 ml vzduchu a poté pístem rotáhla na objem 11 ml. Jak se změní tlak? Jaký předpoklad při výpočtu činíte?
Budeme předpokládat, že teplota na konci bude stejná jako na začátku, tedy že se teploty vyrovnají s okolím. Potom platí
Výsledný tlak 73 kPa.
28. Ve válci motoru je uzavřeno 5 litrů plynu o normálním tlaku a teplotě 20°C. Stlačením pístu se tlak zvýšil na 900 kPa a jeho teplota vzrostla na 250 °C. Jaký byl konečný objem plynu ve válci?
a) 1 litr; b) 0,5 litru; c) 2 litry; d) 1,5 litru
Dva stavy téhož plynu:
Odtud můžeme vyjádřit V2 obecně, ale pro tento případ bude nejpřehlednější rovnou dosadit. Objem můžeme dosadit v litrech – výsledek bude také v litrech. Tlak dosazujeme v kPa, výsledek závisí jen na podílu tlaků.
Máme 100 ⋅ 5 / 293 = 900 ⋅ V2 / 523.
Potom V2 = (100/900) ⋅ (523/293) ⋅ 5 ≈ 0,99 litru ≈ 1 litr.
Konečný objem 1 litr.
29. Teplota plynu ve válci byla zvýšena ze 20°C na 200°C a objem plynu se přitom zvýšil o 1/3. Jak se změnil tlak plynu?
Dva stavy téhož plynu:
Neznáme počáteční tlak, zajímá nás ale jen relativní změna: hledáme podíl
p2/p1 = (V1/V2)
Tedy tlak vroste o 21%. Vidíme, že konkrétně nemáme zadány skoro žádné hodnoty a zajímají nás relativní změny. V takovém případě si klidně můžeme říci: Nechť p1 = 1 Pa, V1 = 1 m3. Potom stavová rovnice je: 1 ⋅ 1/273 = p2 ⋅ (4/3)/473 a snadno vyjádříme p2.
Tlak vroste o 21%.
30. Odvoďte pomocí stavové rovnice, jakou velikost má molární objem při teplotě 25°C a normálním tlaku (tedy objem jednoho molu plynu).
Stavová rovnice: pV = nRT.
Máme p = 101 325 Pa; n = 1 mol; R = 8,31 J mol-1 K-1; T = 298,15 K.
Vše máme v základních jednotkách, můžeme bezproblémově dosazovat. Vyjádříme
V = nRT/p = 1 ⋅ 8,3145 ⋅ 298,15 / 101325 = 0,02447 m3 = 24,47 litrů.
Známe hodnotu 22,4 litrů, molární objem za normálních podmínek, kde je ale T = 0°C. Za zadaných podmínek je tedy přirozeně molární objem o něco větší.
Objem 1 molu plynu 24,47 litrů.
31. Potápěč má tlakovou láhev s kyslíkem o objemu 5 litrů a tlaku 150 atm. Prázdná lahev váží 3 kg. Má šanci potěžkáním rozeznat, zda je láhev plná, nebo prázdná?
Zápis: V = 5 × 10-3 m3; p ≈ 15 × 106 Pa; berme T = 20°C = 293 K.
Stavová rovnice pV = nRT, neznámou je látkové množství
n = pV/RT = … = 30,8 mol.
Molární hmotnost kyslíku Mm = 16 g/mol, tedy
m = n ⋅ Mm = (30,8 mol) ⋅ (16 g/mol) = 493 g.
Hmotnost plynu je zhruba půl kila. To není zanedbatelné proti hmotnosti lahve 3 kg, zkušený potápěč může poznat.
Plyn má hmotnost 493 g, potápěč má šanci to poznat.
32. Vyjádřete vztah mezi hustotou plynu, stavovými veličinami a jeho molární hmotností. Vyjděte z definice hustoty, stavové rovnice a definice molární hmotnosti.
ρ = m/V; pV = nRT; m = nMm.
Kombinací prvního a třetího vztahu vyloučíme hmotnost:
ρ = nMm/V.
Nyní za látkové množství dosadíme ze stavové rovnice n = pV/RT, tedy
33. Ve vznětovém motoru (naftový) se před vznícením směsi objem válce rychle zmenší až 20x v důsledku pohybu pístu (takzvaný kompresní poměr r = 20:1). Jaký tlak a jakou teplotu dosáhne plyn při takovém adiabatickém stlačení, pokud na začátku byl tlak standardní 100 kPa a teplota plynu 80°C?
Při řešení kombinujeme vztah
a stavovou rovnici $p_1V_1/T_1 = p_2V_2/T_2$.
Z prvního vztahu máme
Dosadíme: p2 = 100 kPa ⋅ (20/1)1,4 = 6629 kPa ≈ 6,6 MPa. Ze stavové rovnice potom
Tedy téměr 900°C, což stačí na vznícení palivové směsi.
Tlak 6,6 MPa, teplota asi 900°C.
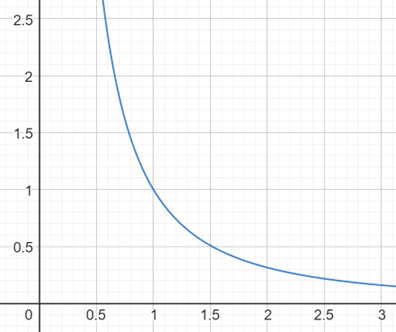
34. Vysvětlete, proč se plyn při adiabatickém stlačování zahřívá. Pokuste se načrtnou graf adiabatického děje v pV diagramu.
Píst jde proti pohybu molekul a při odraze molekuly o píst jí takto urychlí → nárůst teploty plynu. Graf adiabaty je vlastně graf funkce
Práce plynu, tepelné stroje, kruhový děj, tepelné motory

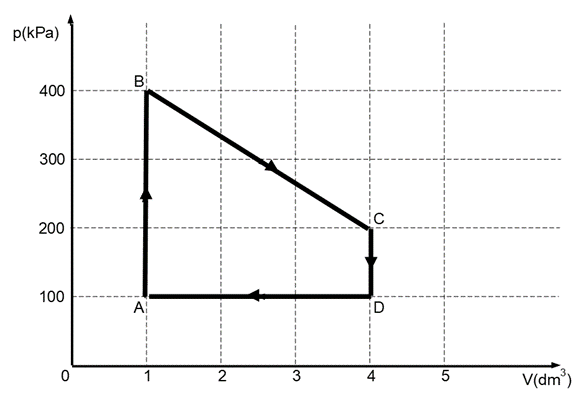
35. V pV diagramu je znázorněn kruhový děj s ideálním plynem uzavřeným ve válci s pístem.
a) Popište jednotlivé děje.
b) Určete, během kterých dějů plyn přijímá/odevzdává teplo a při kterých dějích koná práci / práce je konána na plynu.
c) Určete, zda má plyn větší teplotu ve stavu B nebo C.
d) Určete práci vykonanou při ději B → C.
d) Určete celkovou úhrnnou práci vykonanou plynem během jednoho cyklu tohoto děje.
a) AB: izochorický, BC: není speciální děj, CD: izochorický, DA: izobarická komprese.
b) AB: přijímá teplo, nekoná práci; BC: přijímá teplo, koná práci; CD: odevzdává teplo, nekoná práci; DA: odevzdává teplo, práce je konána na plynu (je stlačován).
c) Větší teplota je ve stavu C (součin pV je zde větší než v B).
d) Průměrný tlak je 300 kPa. Proto W = pΔV = 3×105 Pa ⋅ 3×10-3 m3 = 900 J.
e) V ději DA je vykonána práce na plynu o velikosti pΔV = 300 J. Celková úhrnná práce cyklu tedy 600 J.
Úhrnná práce cyklu 600 J.
36. Spálením 1 kg benzínu v tepelném stroji se uvolní energie asi 47 MJ. Stroj odevzdal chladiči teplo o velikosti 30 MJ. Určete vykonanou užitečnou práci a účinnost stroje.
W = Qin – Qout = 17 MJ. Účinnost η = 17/47 = 0,36 = 36 %.
Práce 17 MJ, účinnost 36%.
37. Popište principy činnosti různých druhů tepelných strojů.
To je na dlouhé povídání…
38. Rozhodněte, zda je tvrzení pravdivé nebo nepravdivé. Nesprávná opravte.
a) Do zážehového motoru se palivo vstřikuje.
b) Při práci vznětového motoru v celém cyklu platí pV/T = konst, protože se jedná různé stavy “téhož” plynu.
c) Fázi stlačení ve vznětovém motoru je možné modelovat jako adiabatickou expanzi.
d) Účinnost parní turbíny je obecně větší než účinnost spalovacích motorů.
e) Účinnost spalovacích motorů je obvykle > 50%.
f) Raketový motor vytváří tah tím, že dochází ke slučování např. kyslíku s vodíkem, při reakci vzniká množství horkého plynu, který uniká tryskou a podle 3. Newtonova zákona poháná raketu.
Správně c, d, f. Ostatní nesprávně.
Pevné látky – struktura, pevnost, pružnost, deformace, teplotní roztažnost
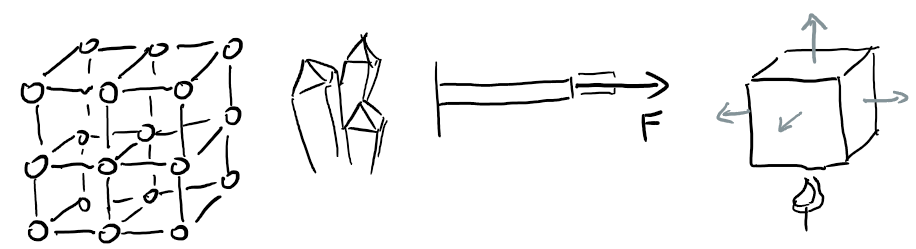
39. Popište různé krystalické formy uhlíku a popište, jak závisí vlastnosti uhlíku na jeho krystalické formě.
Grafit a diamant. Grafit černý, elektricky vodivý, měkký, otírá se. V grafitu kovalentní vazby mezi uhlíky v rámci vrstvy (vazba ke 3 sousedům). Jednotlivé vrstvy k sobě lnou jen nevazebnými interakcemi. Vrstvy se proto otírají. V planárné struktuře grafitu jsou delokalizované elektrony, které se mohou přesouvat na dlouhé vzdálenosti – velmi dobrá elektrická vodivost. Jedna jediná vrstva – moderní materiál grafen. Diamant průhledný, extrémně tvrdý, elektrický izolant. Kovalentní vazba se 4 sousedními uhlíky.
40. Vysvětlete, jaký vliv mohou mít příměsy v krystalu a kde se toho využívá v praxi.
Např. barevnost minerálů a drahých kamenů; Polovodiče – zvýšení vodivosti křemíkového krystalu, polovodiče typu P, N – základ diody a tranzistoru.
41. Vysvětele rozdíl mezi monokrystalickou a polykrystalickou látkou, uveďte příklady.
Polykrystal – “těsný slepenec” malých monokrystalů. Kovy bývají polykrystaly. Viditelné monokrystaly napřř. krystalky kuchyňksé soli nebo umělý monokrystal křemíku pořtebný k výrobě desek mikročipů.
42. Rozhodněte, zda je tvrzení pravdivé či nikoli:
a) V grafitu je uhlík kovalentně vázán ke třem dalším uhlíkům.
b) Diamant má velmi dobrou elektrickou vodivost.
c) Amorfní látky nemají přesně určenou teplotu tání.
d) Beton má výrazně větší odolnost (pevnost) v tahu nežli v tlaku.
e) Elastická deformace je vratná.
f) Látka s velkým modulem pružnosti v tahu se snadno natahuje.
g) Deformaci kovů lze zpravidla popisovat Hookovým zákonem až do překročení meze pevnosti a přetržení.
h) Koeficient teplotní roztažnosti oceli a betonu mají podobnou hodnotu.
i) Koeficienty teplotní roztažnosti plastů a kovů mají podobnou hodnotu.
j) Když zahřejeme kovový prstenec, tak se vnitřní otvor zvětší.
k) Zchlazením kovu jeho hustota klesne.
l) Zahnutý teploměrný bimetalový pásek má kov s vyšší teplotní roztažností na vnějším oblouku.
Správně: a, c, e, h, l.
43. Helmut na stropní traverzu ve skladu plyšáků zavěsil ocelové lanko o průměru 2 mm a délce 2 m. Na lanko se chce pověsit a houpat se.
a) Přetrhne se lanko nebo ne?
b) Pokud ne, o kolik se zatížením prodlouží?
c) Zvažte, zda je k předchozímu výpočtu potřeba nějaký předpoklad a zda je korektní. Potřebné hodnoty si vyhledejte nebo odhadněte.
Uvažujme m = 80 kg → F ≈ 800 N, σp = 400 MPa, modul pružnosti E = 210 GPa.
Máme r = 1 mm, tedy S = 3,14 × 10-6 m2, L0 = 2 m.
Napětí v lanku σ = F/S = 800 N / (3,14 × 10-6 m2) = 255 × 106 Pa = 255 MPa.
To je méně než mez pevnosti a lanko se tedy nepřetrhne.
Prodloužení lanka ΔL = L0 ⋅ σ/E = (2 m) ⋅ (255 × 106 Pa) / (210 × 109 Pa) = 2,4×10-3 m = 2,4 mm.
To je těžko postřehnutelné.
Je výpočet korektní? Výpočet předpokládá, že lze použít Hookův zákon pro elastickou deformaci, tedy že napětí a prodloužení jsou si přímo úměrné, tzn. že napětí je menší než mez úměrnosti. To obecně platí, když je napětí výrazně menší, než mez pevnosti. Zde napětí není násobně menší a bylo by tedy třeba přesněji ověřit.
a) Vznikne napětí 255 MPa, nepřetrhne se. b) Prodloužení 2,4 mm.
44. Jak vysoká může být betonová zeď, aniž by se u základů rozdrtila vlastní vahou? Uvažujme mez pevnosti v tlaku betonu 20 MPa.
Jde o tlak vyvolaný vlastní vahou:
p = F/S = ρhSg/S = ρhg,
tedy podle očekávání je vztah stejný jako hydrostatický tlak (tlak způsobený vlastní tíhou). Vyjádříme výšku stěny
h = p/(ρg).
Hustota betonu asi 2400 kg/m3. Dosadíme v základních jednotkách:
h = p/(ρg) = (20×106)/(2400 ⋅ 9,8) = 850 m.
To je výška nejvyšších pozemských budov, které ale nejsou samozřejmě čistě betonové.
Výška zdi 850 m.
45. Co je to dilatační spára a proč se používá?
Ve stavebnictví a strojírenství – oddělení dvou částí konstrukce mezerou, aby při termální expanzi jednotlivých částí nedocházelo k deformacím a vzniku velkých tlaků.
46. Má varné sklo vyšší nebo nižší koeficient teplotní roztažnosti než normální sklo?
Varné sklo (např. borosilikátové) má nižší koeficient teplotní roztažnosti. Při změně teploty skla může dojít k prasknutí právě kvůli vzniku tlaků/pnutí v materiálu v důsledku teplotního roztažení/smrštění.
47. O kolik se prodlouží patnáctimetrová ocelová kolejnice mezi zimou a létem? *Pokud by byly její konce v zimě fixně připevněny, o kolik se kolejnice vyboulí? Můžete provést přibližný výpočet.
Teplotní rozdíl mezi zimou a létem počítejme řekněme až 50°C. Prodloužení
ΔL = α L0 ΔT = (12×10-6 K-1) ⋅ (15 m) ⋅ (50 K)=9×10-3 m = 9 mm.
*Výpočet velikosti vyboulení d si zjednodušíme. Budeme uvažovat vybočení ne do oblouku, nýbrž do “stříšky”. Řešíme tak pravoúhlý trojúhelník, kde spodní odvěsna má délku 7500 mm, přepona má délku 7504,5 mm a druhá odvěsna je d. Máme pak
Čtvrt metru je dost!
(Kdo umí pracovat s matematickými aproximacemi, tak může také dospět k přibližnému vztahu
Prodloužení asi 9 mm při rozdílu teplot 50°C. Vyboulení asi 26 cm.

48. *Geralt napnul mezi dvě stěny ocelový drát tak, že drát je prakticky vodorovný. Yennefer potom na drát seslala mrazivé kouzlo a drát se smrštil a prasknul. Jaké teploty musel drát dosáhnout, aby se smrštil tolik, že praskne?
Zápis: T0 = 20°C, T1 = ?, σp = 400 MPa, E = 210 GPa, α = 12×10-6 K-1.
Drát praskne, když jeho relativní prodloužení (vzhledem k normální délce při snížené teplotě) vyvolá napětí rovné mezi pevnosti, tedy při relativním prodloužení ε = σp/E.
Relativní prodloužení lze vyjádřit i pomocí teplotní roztažnosti ε = αΔT.
Poslední dva vztahy tak lze dát do rovnosti:
Mrazivé kouzlo muselo zchladit drát o 159°C, tedy řekněme na -139°C.
Kapaliny – povrchové napětí, kapilární jevy, teplotní roztažnost

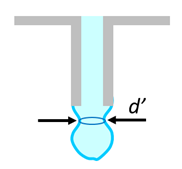
49. Yennefer si do injekční stříkačky (bez jehly) nabrala neznámou kapalinu a postupně ji vytlačovala tak, že voda vykapávala po jednotlivých kapkách. V Aretuze ji totiž učili, že takto může určit povrchové napětí kapaliny. Kapka se odtrhne ve chvíli, kdy převáží tíha kapky nad silou povrchového napětí. K odtrhnutí dochází ve chvíli, kdy je vyznačený průměr d‘ přibližně roven vnitřnímu průměru trubičky. Yennefer, že na odkapání objemu 1 ml odpovídá 25 kapek. Vnitřní průměr trubičky byl přibližně 2 mm.
a) Určete povrchové napětí kapaliny (ve styku se vzduchem) při dané teplotě. Nápověda: Kapku drží povrchová „pružná blána“. Je potřeba vyjádřit „délku“ této blány.
b) Mohlo by se jednat o obyčejnou vodu?
c) Co kdyby byla teplota kapaliny větší? Jak by se změnilo povrchové napětí? Odpovídalo by jednomu mililitru více kapek nebo méně kapek.
Zápis: d = 2 mm = 2×10-3 m; hmotnost kapky m = 1 g / 25 = 0,04 g = 4×10-5 kg;
délka blány je obvod kruhu L = πd = 6,3 mm = 6,3×10-3 m.
Při odtrhávání platí, že tíha kapky (síla směrem dolů) je shodná se silou pružnosti blány (síla nahoru):
mg = σL. Odtud σ = mg/L = (4×10-5 kg) ⋅ (9,8 N/kg) / (6,3×10-3 m) = 6,2×10-2 N/m = 62 mN/m.
Voda má podle tabulek povrchové napětí 73 mN/m při 20°C. Vzhledem k nepřesnostem měření a metody by se klidně mohlo jednat o vodu. Kdyby byla teplota vyšší, soudržnost molekul bude nižší, povrchové napětí bude nižší a stačí menší kapka na odtržení – tedy kapek bude víc.
Povrchové napětí ca. 62 mN/m.
50. Jaký tvar má padající kapka deště? Které efekty ovlivňují tvar kapky? Na čem tvar kapky závisí?
Kapka nemá tvar jak se obyčejně kreslí. Malá kapka (průměr 1 mm) je kulová v důsledku sil povrchového napětí). Větší kapky jsou deformovány odporem vzduchu více doplacata.
51. Vysvětlete pojmy kohezní a adhezní síly.
Kohezní – přilnavé síly svůj k svému (např. voda – voda); adhezní – jedna látka k jiné (např. voda-sklo).
52. Na rámu s pohyblivou příčkou s délkou 5 cm je mýdlová bublina (povrchové napětí blány je 35 mN/m). Jakou práci je třeba vykonat, aby se příčka posunula o 2 cm?
Zápis: L = 5 cm; σ = 40 mN/m; s = 2 cm.
Blána má dva povrchy – spodní a vrchní. Síla povrchového napětí je F = 2Lσ. Práce je potom
W = F⋅ s = 2Lσs = 2 ⋅ (5×10-2 m) ⋅ (35×10-3 N/m) ⋅ (2×10-2 m) = 70 μJ.
To je docela maličká energie v makroskopických rozměrech. Velkého významu nabývá povrchové napětí až na malých rozměrech, kde podíl plochy povrchu vůči objemu a hmotnosti narůstá.
Práce 70 μJ.
53. *Mějme dvě miniaturní bublinky ve vodě, každou o poloměru 1 nm. Jak velká energie se uvolní při jejich spojení (sloučení) do jedné větší bublinky? Vyjádřete v jednotce kJ/mol, tedy kolik energie by se uvolnilo sloučením jednoho molu bublinek. Pro srovnání, při vzniku 1 molu C-C vazeb se uvolní energie 346 kJ/mol.
Jaký bude poloměr nové bublinky? Objem bude 2x větší a objem roste s třetí mocninou poloměru, tedy poloměr vzroste 21/3 ≈ 1,26 krát. O kolik se zmenší celkový povrch sloučením bublinek?
Změna povrchové energie na jedno sloučení pak je ΔE = ΔS ⋅ σ. Na 1 mol máme
ΔE = ΔS ⋅ σ ⋅ NA. Dosazením dostaneme 228 kJ/mol.
To je srovnatelné s energií C-C vazby. Síla povrchového napětí může být na miniaturních rozměrech velmi významná. Je to proto, že při zmenšování objektu roste podíl povrch/objem, potažmo povrch/hmotnost.
Uvolení se povrchová energie o velikosti 228 kJ/mol.
54. Vystoupí voda výš ve skleněné kapiláře o průměru 1mm nebo 0,5 mm?
Výš vystoupí v tenčí kapiláře.
55. Jak je možné zařídit, aby povrch byl nesmáčivý? Jak vypadá kapka, která leží na smáčivém/nesmáčivém materiálu? Kde se v praxi a přírodě setkáváme s nesmáčivými materiály?
Povrch lze třeba navoskovat či opatřit impregnací. Také může mít povrch složitou mikrostrukturu (výčnělky, sloupečky, lamely) – toho využívají třeba křídla motýlů, ze kterých musí voda účinně stékat dolů.
56. Jak vypadá molekula fosfolipidu? Jaké struktury fosfolipidy vytváří ve vodě? Jaký to má význam pro život?
Polární fosfátová hlavička, nepolární lipidový ocásek. Nepolární ocásky se ve vodném prostředí organizují k sobě, zatímco hlavičky koukají ven do vodného prostředí. Samovolně se tak ve vodě vytvoří struktury jako micely či dvojvrstvy. Základ života – buněčná membrána.
57. Jak se změní objem vody, pokud ji zchladíme z 10°C na 4°C? A při dalším zchlazení ze 4°C na 1°C? Co když pak voda zmrzne? Jak se mění hustota?
Z 10°C na 4°C se objem zmenší (anomálie vody – max. hustota při 4°C). Ze 4°C na 1°C se naopak trošičku objem zvětší. Při ztuhnutí se objem skokově zvětší (menší hustota – led 917 kg/m3).
58. Stolitrový hliníkový sud je až po okraj naplněn vodou, přičemž teplota je 15°C. Kolik vody ze sudu vyteče, když se oteplí na 35°C?
Koeficient objemové roztažnosti vody asi β = 207 × 10-6 K-1. Změna objemu vody je
ΔV = V0βΔT = (100 L) ⋅ (190 × 10-6 K-1) ⋅ (20 K) = 0,414 litru.
Nutno uvážit, o kolik se zvětší objem hliníkového sudu. Délková roztažnost hliníku 23 × 10-6 K-1, objemový koeficient tedy trojnásobek: 69 × 10-6 K-1. Proto objem sudu vzroste o 0,138 litru.
Vyteče tedy 0,276 litru vody.
Změny skupenství – tání, tuhnutí, sublimace

59. Charakterizujte různá skupenství na základě sil mezi molekulami.
Plyny žádné nebo velmi slabé síly (kvůli velkým vzdálenostem molekul). Pevné látky mají částice v rovnovážných polohách. Při vychýlení z rovnovážné polohy se objeví významné síly, které částici vrací zpět. V kapalinách jsou částice také v rovnovážných vzdálenostech, ale poměr kinetické energie částic k vazebné energii je takový, že je umožněno přesmýkání částic.
60. V parném létě si Pepíček chce ochladit litr minerálky o počáteční teplotě 30°C. Limonádu tedy dal do termosky a chce k ní přidat led z mrazáku, který má počáteční teplotu -18°C. Kolik musí přidat ledu, aby se teplota nápoje v termosce ustálila na konečných 10°C? Tepelnou kapacitu vlastní termosky zanedbejte, předpokládejte dokonalou tepelnou izolaci.
Minerálka má prakticku stejné vlastnosti jako voda, i měrnou tepelnou kapacitu. Pro přehlednost minerálku značíme indexem “m”, vodu “v” a led “L”. Hmotnost zmrzlé vody značíme jednoduše m. Litr minerálky, tedy kilo minerálky. Voda z mrazáku bude odebírat teplo z minerálky. Z minerálky je třeba odebrat teplo
Qout = mm cm ΔT = (1 kg) ⋅ (4,2 kJ/kg/K) ⋅ (20 K) = 84 kJ.
Toto teplo přijme voda z mrazáku:
Qout = Qin=mcL⋅18 K + mlt + mcv⋅10 K = m(cL⋅18 K + lt + cv⋅10 K).
Konečně hmotnost zmrzlé vody z mrazáku:
m = (84 kJ) / (cL⋅18 K + lt + cv⋅10 K).
Dosadíme za tepelné kapacity v kJ a máme m = 0,203 kg = 203 g ledu.
Musí přidat asi 203 g ledu.
61. Diabolky do vzduchovky se dělají (dělávali) z olova. Jakou minimální rychlostí by diabolka musela narazit na pancéřovou stěnu, aby se diabolka roztavila? Řešte nejprve obecně, všechny veličiny řádně označte a pojmenujte. Poté dosaďte konkrétní hodnoty. Uveďte, jaké předpoklady při výpočtu využíváte.
Kinetická energie se přemění na vnitřní energii diabolky, tedy spotřebuje se na zahřátí z T0 na Tt a následnou skupenskou změnu. Předpokládejme pro jednoduchost, že veškerá energie zůstane v diabolce a nepřejde do stěny. Pro mezní rychlost bude platit
Dosazením konkrétních hodnot pro olovo (základní jednotky):
To je nadzvuková rychlost, kterou běžná vzduchovka určitě nevyvine. Předpokládali jsme také, že se měrná tepelná kapacita při zahřívání nemění, což není úplně fyzikální pravda.
Min. rychlost 353 m/s pokud veškerá energie zůstane v diabolce.
62. Seřaďte látky vzestupně podle teploty tání: parafín, rtuť, voda, SiO2, wolfram, cín, železo, bronz, SiC.
rtuť, voda, parafín, cín, sklo, bronz, železo, SiO2, SiC, wolfram.
63. Uveďte příklady látek, které mají tendenci sublimovat.
Jód, naftalen, suchý led, vonné látky.
64. Možná jste někdy viděli hřejivý polštářek: nejdříve se nahřeje, obsah se stane tekutým. Potom trochu schladne. Pak uvnitř polštářku ohneme takový plíšek a tekutina začne tuhnout do krystalů. Při tuhnutí obsahu se polštářek zahřívá? Proč?
Látka v polštářku byla v kapalném stavu, ale pod teplotou tuhnutí. Vznik krystalizačního centra v důsledku ohnutí plíšku zahájí krystalizaci, při které se do okolí uvolní skupenské teplo tání/tuhnutí.
65. Jak se mění objem vody při tuhnutí? Jaké to má implikace v přírodě/praxi? Jak se objem mění při tuhnutí jiných látek?
Objem vzroste zhruba o 9%. Hustota vody 1000 kg/m3, hustota ledu 917 kg/m3. Voda je spíš vyjímkou, jiné látky při ztuhnutí spíše zmenší objem – pevnější uspořádání částic.
66. Proč se v zimě solí silnice?
Směs voda-sůl má výrazně nižší teplotu tání než samotná voda, klidně výrazně pod -10°C. Tedy slaná voda zůstává kapalná i při nízkých teplotách (v přítomnosti soli je totiž pro vodu obtížnější vytvořit pravidelnou krystalickou mříž). Když do ledu přisypeme sůl, tak sůl “odtrhává” molekuly vody z ledu a zároveň disociuje na ionty Na+ a Cl–. Tento proces probíhá samovolně, protože při něm roste entropie – neuspořádanost (původně uspořádaný systém kousek ledu – kousek soli se mění na neuspořádaný promíchaný systém). Zároveň je ale disociace soli endotermický proces, tedy odebírá energii z okolí, v důsledku čehož se snižuje teplota systému – směs chladne.
67. Co bývá obvykle složkou nemrznoucích kapalin?
Přidává se zejména alkoholy, jako etanol, metanol, isopropanol, ethylenglycol,…
68. Co je to přechlazená kapalina?
Kapalina pod teplotou tuhnutí. Stačí vznik krystalizačního centra a kapalina může skokově ztuhnout, přičem uvolní skupenské teplo tuhnutí.
Změny skupenství – vypařování, var, sytá pára, kondenzace

69. Mějme rychlovarnou konvici o výkonu 1,5 kW. Určete, za jak dlouho se úplně přemění v páru půl litru vody o pokojové teplotě. Potřebné hodnoty si vyhledejte.
Zápis: P = 1,5 kW; c = 4,2 kJ/kg/K; lt = 2257 kJ/kg/K; m = 0,5 kg; T0 = 20°C.
Budeme-li počítat s kilowatty a kilojouly, tak se nám „kilo“ vykrátí a výsledek bude korektní v základních jednotkách. Hledaný čas je
t = Q / P = m(cΔT + lt) / P = 0,5 ⋅ (4,2 ⋅ 80 + 2257) / 1,5 = 864 s = 14 min 24 s.
Vyvaří se za 14 min 24 s.
70. Jaké jsou přibližné teploty varu vody, ethanolu, methanolu, kuchyňského oleje za normálního tlaku? Proč je to zajímavé (podstatné)?
Voda 100°C, etanol 78°C, metanol 65°C. Je to podstatné při destilaci – směs se zahřívá na teploty okolo 80°C – 95°C, aby se preferenčně odpařil etanol. Pozor, nejrychleji se vypařuje metanol a počáteční výtěžek destilace je potřeba proto vyhodit. U kuchyňských olejů (např. olivový), se spíše udává kouřový bod, např. pro olivový kouřový bod ~200°C, bod varu až 299°C. Nad kouřovým bodem začne olej hodně kouřit a smrdět.
71. Jak se zajistí, aby destilát obsahoval co nejméně metanolu?
Zlikviduje se prvotní výtěžek destilace, protože metanol má nejnižší bod varu a nejlépe se vypařuje.
72. Co to znamená, když kapalina je těkavá?
Snadno se odpařuje, relativně slabé meizmolekulární síly, relativně nízká teplota varu.
73. Jaký je rozdíl mezi vypařováním a varem?
Var – vypařování z celého objemu. Var nastává při teplotě, kdy tlak sytých par odpovídá okolnímu tlaku. Potom miniaturní bublinka par uvnitř kapaliny může růst, protože vnitřní tlak sytých par v bublince překoná vnější tlak.
74. Na čem závisí rychlost vypařování?
Druh kapaliny (velikost mezimolekulárních sil), teplota, velikost povrchu, odvětrávání.
75. Co je to sytá pára? Za jakých okolností vznikne sytá pára?
V uzavřené nádobě nad hladinou kapaliny vznikne sytá pára o určitém tlaku. V tomto stavu je počet molekul opouštjěících kapalinu stejný jako počet molekul, které se z plynného stavu do kapaliny vrací. Úhrnné množství látky v plynném stavu tedy již dále nenarůstá.
76. Když bychom zblízka pozorovali kapalinu, která přejde kritickou teplotu, co bychom viděli?
Ztratí se hladina, tedy ztratí se viditelné rozhraní mezi kapalinou a plynem.
77. Z čeho jsou mraky? Proč jsou bílé?
Teplý vlhký vzduch od povrchu země stoupá vzhůru. Ve vyšších polohách je nižší teplota. Dojde ke kondenzaci par na kapičky, v ještě vyšších polohách vznik ledových krystalků. Kapičky i krystalky jsou sami o sobě průhledné, ale velké množství malých průhledných objektů rozptyluje světlo (mnohočetné odrazy světla). Mraky pak odráží zhruba rovnoměrně všechny barvy a jeví se bílé.
78. V podrobné předpovědi počasí je možné se dočíst, že dnes je rosný bod třeba 15°C. Souvisí to s vlhkostí vzduchu. Co to znamená?
Ve vzduchu je obsaženo určité množství vodní páry (udává se v g/kg, tedy gramů páry na kilo vzduchu). Řekněme, že při 30°C bude ve vzduchu obsaženo 10 g/kg vodní páry, což při této teplotě odpovídá 40% vlhkosti. Při nižší teplotě však vzduch nepojme tolik páry v plynném stavu. Rosný bod 15°C znamená, že při této teplotě dané množství páry v g/kg odpovídá 100% vlhkosti a při dalším snížení teploty se pára začíná srážet – vznik rosy.
79. Uveďte příklady z přírody či praxe, kdy dochází ke kondenzaci.
Zavřená sklenice s vodou, kterou dáme do lednice. Vlhký teplý vzduch při poklesu teploty nad ránem kondenzuje do rosy. Lednice – stlačením média dochází k jeho kondenzaci a uvolnění skupenského tepla, což je jedna z fází přenosu tepla zevnitř lednice směrem ven.
80. Proč nás chladí, když se potíme? Bude nás víc chladit, když se polijeme vodou nebo lihem?
Nejrychlejší molekuly vody odcházejí a tedy zbytek vody má molekuly v průměru pomalejší, což odpovídá nižší teplotě. Odpar lihu ochlazuje intenzivněji, protože je rychlejší (líh je těkavější).
81. Je teplota varu vody v horách vyšší nebo nižší než obvykle? Uvaří se tam vajíčko rychleji nebo pomaleji?
Na horách je nižší teplota varu v důsledku nižšího atmosferického tlaku. Ve výšce okolo 8000 mnm je tlak asi 40 kPa a teplota varu zhruba 70°C. Vajíčko se ve vodě o teplotě 70°C bude vařit mnohem déle, protože se bude pomaleji prohřívat. Navíc se udává, že pro úplnou přeměnu žloutku do jeho “pevné podoby” je potřeba teplota 72°C.
82. Zemní plyn se pro převoz a skladování zkapalňuje. Co je potřeba udělat ke zkapalnění? Je možné, aby byla zkapalněna vodní pára při teplotě 120°C?
Je nutné plyn dostat pod jeho kritickou teplotu, aby vůbec šlo mluvit o kapalině či plynu. I při podkritické teplotě však sytá pára nad kapalinou může mít hodně velký tlak a bylo by tak potřeba skladovat zkaplněný pltn v tlakových nádobách při vysokém tlaku. Pokud chceme skladovat za běžného tlaku, tak je potřeba zchladit pod teplotu varu při atm. tlaku. Pro metan (zemní plyn) je kritická teplota -82,6°C a kritický tlak 46 atm. Teplota varu za normálních podmínek je -161,6°C, takže je třeba metan zchladit pod tuto teplotu, aby bylo možno skladovat za normálního tlaku. Ano, vodu by bylo možné zkapalnit při teplotě 120°C, tedy nad bodem varu, ale potřebovali bychom vyšší tlak než atmosferický.